Exercícios de Física para o 1º ano do Ensino Médio
Aqui você encontra exercícios variados de Física para você treinar os conhecimentos adquiridos no primeiro ano do Ensino Médio.
Publicado por: Thiago Tavares da CostaQuestões
-
Questão 1
(Unicamp 2025) Mudanças climáticas têm influenciado correntes de ar na alta atmosfera. Em particular, na região do Atlântico Norte, onde ventos fortes geralmente sopram de oeste para leste, os tempos de voos têm sofrido alterações. Em uma viagem de Baltimore (EUA) a Londres (Reino Unido), o tempo total de voo é igual a oito horas quando não há vento em toda a trajetória. Considere agora uma viagem subdividida em três trechos (A, B e C), conforme a figura a seguir. No trecho B, na direção de oeste para leste, há vento com velocidade constante de módulo \( |\vec V_{vento,\ solo}| -250\ km/h \) em relação ao solo.
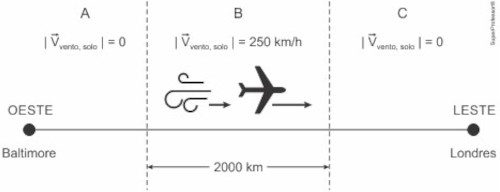
Sendo, nos três trechos, o módulo da velocidade média do avião em relação ao vento \( |\vec V_{vento,\ solo}| -750\ km/h \) podemos afirmar que:
a) o módulo da velocidade média do avião em relação ao solo no trecho B é \( |\vec V_{avião,\ solo}| -500\ km/h \) e o tempo de viagem no mesmo trecho é \(\Delta t=4,0h\).
b) o módulo da velocidade média do avião em relação ao solo no trecho B é \( |\vec V_{avião,\ solo}| -500\ km/h \) e o tempo de viagem no mesmo trecho é \(\Delta t=2,0h\).
c) o módulo da velocidade média do avião em relação ao solo no trecho B é \( |\vec V_{avião,\ solo}| -1000\ km/h \) e o tempo de viagem no mesmo trecho é \(\Delta t=4,0h\).
d) o módulo da velocidade média do avião em relação ao solo no trecho B é \( |\vec V_{avião,\ solo}| -1000\ km/h \) e o tempo de viagem no mesmo trecho é \(\Delta t=2,0h\).
Resposta:
[D].
O avião está sujeito a duas velocidades de mesmo sentido, então:
\( |\vec V_{avião,\ solo}| = |\vec V_{avião,\ vento}| + |\vec V_{vento,\ solo}| \Rightarrow (750+250)km/h \therefore |\vec V_{avião,\ solo}| = 1000 km/h\)
Aplicando a definição de velocidade média, o tempo para percorrer o trecho B é:
\(\Delta t=\frac{\Delta S_B}{V_{avião,\ solo}}=\frac{2.000}{1.000} ∴ Δt=2h. \)
-
Questão 2
(Famerp 2024) Em uma cobrança de pênalti, um jogador de futebol chuta a bola em direção ao gol com velocidade média de 108 km/h. A partir do momento em que perde contato com o pé do jogador, a bola demora apenas 0,4 segundo para chegar à linha do gol. Durante esse período, a distância percorrida pela bola foi de:
a) 15 m.
b) 14 m.
c) 11 m.
d) 10 m.
e) 12 m.
[E].
\(v_m=108\ km/h=\frac{108}{3,6} m/s ⇒ v_m=30m/s\)
\(d=v_m\Delta t=30\cdot 0,4 \Rightarrow d=12m \)
-
Questão 3
(Uerj 2024) A noção de tempo é fundamental. A sociedade é atual, mas a paisagem, pelas suas formas, é composta de atualidades de hoje e do passado. O espaço construído que daí resulta é variado. Formas de idades diferentes, com finalidades e funções múltiplas, são organizadas e dispostas de diversas maneiras. Cada movimento da sociedade lhes atribui um novo papel.
Adaptado de SANTOS, Milton. Pensando o espaço do homem. São Paulo: Edusp, 2007.
O menor tempo medido em laboratório ocorreu na escala de zeptossegundos e corresponde ao Intervalo Δt em que uma partícula de luz percorre a distância que separa os centros atômicos de uma única molécula de hidrogênio. Uma unidade de zeptossegundo equivale a 10–21 segundo. Admita que a velocidade da luz seja de 3×108 m/s e que a distância entre os centros atômicos de uma molécula de hidrogênio seja de 7,2×10-11 metro.
Nessas condições, no referencial da partícula de luz, o valor de Δt, em zeptossegundos, é igual a:
a) 120
b) 180
c) 240
d) 320
[C].
Resposta do ponto de vista da disciplina de Física:
O intervalo de tempo medido em zeptossegundos equivale a:
\(c=\frac{\Delta s}{\Delta t}\\ 3\cdot 10^8=\frac{7,2\cdot 10^{-11}}{\Delta t}\\ \Delta t=2,4\cdot 10^{-19} s=240\cdot 10^{-21} s\\ \therefore \Delta t=240 zs\)
-
Questão 4
(UFPR 2024) Um objeto de massa m constante move-se num movimento retilíneo uniformemente variado unidimensional descrito pela equação x = -3 + 5t + 2t2, em que x é a posição do objeto, medida em quilômetros, e t é o tempo, medido em horas.
Considerando as informações apresentadas, assinale a alternativa que apresenta corretamente o valor da aceleração a do objeto nesse movimento.
a) a = 1 km/h2
b) a = -3 km/h2
c) a = 2 km/h2
d) a = 5 km/h2
e) a = 4 km/h2
[E].
Comparando a função dada com a função horária do espaço, no MUV:
\(x = x_0 + v_0 t + \frac{a}{2} t^2 \quad \Rightarrow \quad \left\langle \begin{array}{l} x_0 = -3 \ \text{km} \\ v_0 = 5 \ \text{km/h} \\ \frac{a}{2} = 2 \ \Rightarrow \ a = 4 \ \text{km/h}^2 \end{array} \right. \)
-
Questão 5
(FCMSCSP 2023) A distância de frenagem é a mínima distância que um veículo percorre para conseguir parar completamente antes de atingir um obstáculo. Essa distância é a soma da distância de reação, que é a distância percorrida entre o instante que o condutor avista o obstáculo e o instante em que aciona o sistema de freios do veículo, com a distância de parada, que é a distância percorrida pelo veículo após o acionamento dos freios até sua parada total. A figura representa a distância de frenagem típica para um automóvel que trafega com velocidade de 112 km/h, que corresponde a, aproximadamente, 30 m/s.

Considerando que o veículo percorra a distância de reação em movimento uniforme e a distância de parada em movimento uniformemente variado, a aceleração escalar do veículo, durante a distância de parada, é de, aproximadamente,
a) 6,0 m/s2.
b) 7,5 m/s2.
c) 2,5 m/s2.
d) 4,7 m/s2.
e) 12,0 m/s2.
[A].
Aplicando a equação de Torricelli para o trecho em que o veículo está em movimento uniformemente variado, obtemos:
\(v^2=v_0^2+2a\Delta s\\ 0=30^2+2a\cdot 75\\ \therefore a=-6 m/s^2\)
-
Questão 6
(Unicamp 2023) O balonismo, um esporte aeronáutico com adeptos em todo o mundo, oferece um belo espetáculo para os observadores no solo. Um maçarico é usado para aquecer o ar no interior do balão, o que faz variar a densidade do ar, permitindo o controle do movimento de subida e descida do balão.
Um balão, inicialmente em repouso no solo, decola e sobe em movimento uniformemente variado. Se o balão atinge a altura h = 80 m após um tempo t = 40 s, conclui-se que a aceleração vertical do balão nesse movimento é igual a
a) 2,0 m/s2.
b) 4,0 m/s2.
c) 0,05 m/s2.
d) 0,1 m/s2.
[D].
Aplicando a equação horário do espaço:
\(\Delta S=v_0t+\frac{a}{2}t^2 \Rightarrow h=\frac{a}{2}t^2 \Rightarrow 80=\frac{a}{2}(40)^2 \Rightarrow 80=800a \Rightarrow a=0,1m/s^2 \)
-
Questão 7
(PUC-RJ 2023) O gráfico descreve a posição de um carro ao longo do tempo, em uma estrada sem curvas. Os segmentos BC e DE no gráfico são retilíneos.
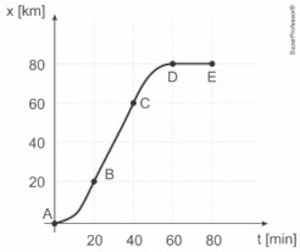
Analisando-se o gráfico, conclui-se que:
a) a velocidade do carro no ponto B é 60 km/h.
b) o carro tem velocidade crescente entre os pontos A e B e entre os pontos C e D.
c) a velocidade no ponto D é 80 km/h.
d) entre os pontos D e E, o carro se desloca com velocidade constante.
e) a velocidade média do carro entre os pontos A e E é 60 km/h.
[E].
[A]. Falsa. Utilizando o trecho BC, obtemos a velocidade no ponto B:
\(v_B=\frac{40 km}{\frac{20}{60} h}=120 km/h\)
[B]. Falsa. A velocidade é decrescente entre os pontos C e D.
[C]. Falsa. A velocidade no ponto D é nula.
[D]. Falsa. Entre os pontos D e E, o carro encontra-se parado.
[E] Verdadeira. A velocidade média entre os pontos A e E foi de:
\(v_B=\frac{80 km}{\frac{80}{60} h}=60 km/h\)
-
Questão 8
(UFPR 2025) Um objeto de massa constante m = 0,2 kg desloca-se em um movimento unidimensional ao longo de uma linha reta, e sua aceleração a é medida em função do tempo t, obtendo-se, então, o gráfico a seguir:
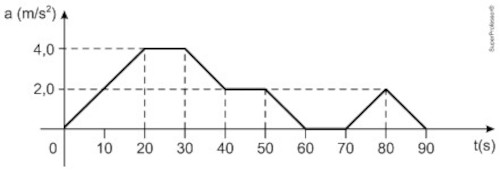
Considerando os dados expostos no enunciado e no gráfico, assinale a alternativa que apresenta corretamente a intensidade F da força resultante aplicada sobre a partícula no instante t = 30 s.
a) F = 0,0 N
b) F = 0,4 N
c) F = 0,8 N
d) F = 4,0 N
e) F = 8,0 N
[C].
Aos 30 segundos a partícula registra no gráfico uma aceleração de 4,0 m/s2, assim, aplicando-se a esses valores a 2ª lei de Newton, também conhecida como princípio fundamental da dinâmica, tem-se o módulo da força resultante nesse instante de tempo:
\(F_R=m\cdot a\\ F_R=0,2 kg\cdot 4,0 m/s^2\\ \therefore F_R=0,8 N\)
-
Questão 9
(UFRGS 2024) Na figura abaixo, estão representados dois corpos de massas M e m, com M > m, unidos por um fio inextensível e de massa desprezível que passa por uma polia, também de massa desprezível e sem atrito.
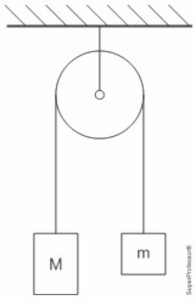
Sendo g o módulo da aceleração da gravidade local, o módulo da aceleração de qualquer um dos dois corpos é dado por:
a) (M – m)g / (M + m).
b) (M – m)g / m.
c) Mg /m.
d) mg / (M + m).
e) Mg / (M + m).
[A].
Aplicando o princípio fundamental da dinâmica ao sistema:
\(F_R=Mg-mg \Rightarrow (M+m) |a|= (M-m)g \therefore |a|= \frac{M-m}{M+m}g. \)
-
Questão 10
(PUC-PR 2024) A Mecânica Newtoniana é baseada em três princípios fundamentais, as chamadas Leis de Newton, estabelecidas pelo físico inglês em seu monumental livro “Princípios Matemáticos da Filosofia Natural”, publicado primeiramente em 1687. A respeito das Leis de Newton e suas aplicações, analise as afirmativas a seguir.
I. De acordo com a 1ª Lei de Newton, ou Princípio da Inércia, um corpo tem a tendência de manter seu estado de repouso ou movimento retilíneo uniforme, a menos que seu estado seja alterado por uma ou mais forças.
II. Conforme a 2ª Lei de Newton, em determinado instante de tempo, a velocidade de uma partícula possui sempre a mesma direção e sentido que a força resultante sobre ela nesse mesmo instante.
III. A força peso de um objeto e a força normal aplicada sobre ele por uma superfície de contato, podem, em algumas situações, formarem um par de ação e reação.
É (São) CORRETA(S) apenas
a) I e II
b) I
c) I e III
d) II
e) II e III
[B].
[I]. Verdadeira. A 1ª Lei de Newton, ou princípio da inércia, trata de situações em que a força resultante sobre um corpo é nula, implicando um estado de repouso ou movimento retilíneo uniforme.
[II]. Falsa. É a aceleração do corpo que possui a mesma direção e sentido da força resultante sobre o corpo.
[III] Falsa. Nunca o peso e a força normal formam um par de ação e reação. A reação ao peso está no centro da Terra e a reação ao contato entre um corpo e a superfície de apoio está na superfície de acordo com a 3ª Lei de Newton.
-
Questão 11
(UFSCAR / Unicamp indígena 2023) Um objeto de 2 kg sofre a ação de várias forças (ilustradas pelo diagrama de corpo livre da figura a seguir).
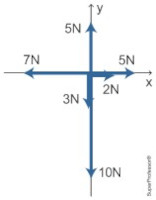
A aceleração do objeto é
a) positiva na direção x e tem magnitude igual a 5 m/s2.
b) positiva na direção y e tem magnitude igual a 2,5 m/s2.
c) negativa na direção x e tem magnitude igual a 3,5 m/s2.
d) negativa na direção y e tem magnitude igual a 4 m/s2.
[D].
Calculando o valor algébrico da resultante das forças em cada eixo:
\(\left. \begin{array}{l} R_x = 5 + 2 - 7 \Rightarrow R_x = 0 \\ R_y = 5 - 3 - 10 \Rightarrow R_y = -8 \ \text{N} \end{array} \right\} \quad \Rightarrow \quad R = R_y = -8 \ \text{N} \) (em sentido oposto ao do eixo y)
A aceleração tem o mesmo sentido da resultante. Aplicando o princípio fundamental da dinâmica:
\(R = m a \;\Rightarrow\; a = \frac{R}{m} = \frac{-8}{2} \;\Rightarrow\; a = -4 \ \text{m/s}^2 \;\Rightarrow\; \boxed{|a| = 4 \ \text{m/s}^2} \) (em sentido oposto ao do eixo y)
-
Questão 12
(UFRGS 2023) Um bloco de 6 kg desliza, sem atrito, sobre uma superfície plana horizontal, tracionado por um bloco de 4 kg que está suspenso por uma corda inextensível e de massa desprezível, que passa por uma roldana, conforme mostra a figura.
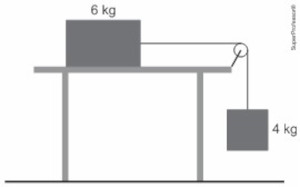
Dados: Use g = 10 m/s2 (módulo da aceleração da gravidade). Considere a roldana sem massa e girando sem atrito.
De quanto é a força de tração na corda?
a) 24,0 N.
b) 30,0 N.
c) 20,0 N.
d) 28,5 N.
e) 14,5 N.
[A]
Isolando os blocos, temos:
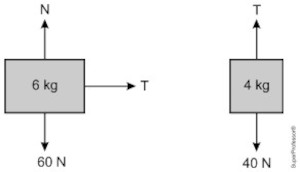
\(\left\{ \begin{array}{l} T = 6a \quad \text{(I)} \\ 40 - T = 4a \quad \text{(II)} \end{array} \right. \)
Fazendo (I) + (II):
\(40 = 10a\)
\(a=4 m/s^2\)
Logo, a tração na corda vale:
\(T=6\cdot 4\)
\(T=24 N\)
-
Questão 13
(Fuvest 2023) Um astronauta está em treinamento no avião que simula gravidade zero realizando voos parabólicos em alta atmosfera, com subidas íngremes e mergulhos acentuados. Em algumas etapas do voo, o astronauta "descola" do chão da aeronave e flutua como se estivesse no espaço.

Nessas condições, é correto afirmar:
a) O peso do astronauta é anulado pela sustentação do avião.
b) O peso do astronauta é duplicado pela sustentação do avião.
c) Durante o mergulho, avião e astronauta estão em queda livre.
d) A força normal sobre o astronauta diminui pela metade durante o mergulho.
e) A força centrífuga é responsável por anular o peso do astronauta.
[C].
Para que o astronauta flutue dentro do avião, ambos devem estar em queda livre, em que:
\(F_{res}=P\\ ma = mg\\ a = g\)
-
Questão 14
(PUC-RJ 2022) Uma bola, quando disparada na Terra com um ângulo de 45 graus em relação ao solo e com uma velocidade inicial de módulo 10 m/s, descreve uma trajetória parabólica.
Na parte mais alta da trajetória, desprezando-se todas as forças dissipativas, a força resultante que atua sobre a bola:
a) é nula.
b) aponta para o mesmo sentido da trajetória.
c) aponta para baixo.
d) aponta para cima.
[C].
Após o disparo, desprezando as forças dissipativas, o objeto estará apenas sob a ação da gravidade, o que faz com que a resultante sobre ele esteja apontada para baixo.
-
Questão 15
(Acafe 2020) Um trenó de neve é puxado por oito cachorros, realizando um movimento retilíneo com velocidade de módulo constante em uma estrada horizontal. Na figura abaixo, pode-se vê-lo de cima. Sobre o trenó estão: um homem, carnes sobre panos, alguns troncos de árvore e uma caixa.
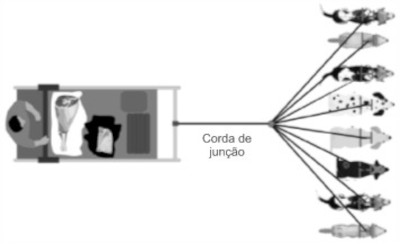
Com base no exposto e desconsiderando as massas das cordas e a resistência do ar, assinale a alternativa correta.
a) Todos os cachorros aplicam sobre o trenó forças de mesma intensidade.
b) A força normal sobre o trenó tem maior módulo que a força peso do trenó.
c) Sobre o trenó não existe força de atrito.
d) O módulo da força resultante sobre o trenó é a soma das forças aplicadas pelos cachorros sobre as cordas.
[B]
Ilustrando as forças que agem sobre o trenó, temos:
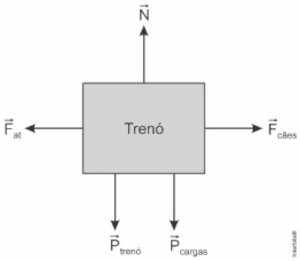
Como o trenó descreve um MRU, a resultante das forças que agem sobre ele deve ser nula. Logo, na vertical, devemos ter:
\(N=P_{trenó}+P_{cargas}\)
Portanto, podemos concluir que a força normal sobre o trenó tem maior módulo que a força peso do trenó.