Exercícios sobre pressão em um fluido
Teste seus conhecimentos por meio desta lista de exercícios sobre a ação da pressão em um fluido.
Publicado por: Thiago Tavares da CostaQuestões
-
Questão 1
Um projeto de engenharia prevê, para o abastecimento de água de um edifício de 10 andares, a instalação de uma caixa d’água na cobertura para que a gravidade atue na distribuição para as unidades abaixo. Pensativa sobre a eficiência, uma pessoa pergunta ao engenheiro se haveria diferença na vazão de água entre apartamentos de uma mesma coluna. O engenheiro respondeu corretamente que:
A) a pressão do tubo do 6º andar é menor, pois, em comparação ao 2º andar, teria uma coluna de água menor.
B) a pressão do tubo do 6º andar é maior, pois, em comparação ao 2º andar, o líquido perderia mais velocidade pelo atrito com a tubulação.
C) a pressão do tubo do 6º andar é maior, pois ele está muito mais próximo da caixa d’agua, logo, a energia potencial seria maior.
D) a pressão em ambos os andares é a mesma, pois o líquido está em equilíbrio hidrostático.
Alternativa A.
A pressão de um líquido em repouso depende de forma diretamente proporcional da altura de sua coluna (p = p0 +ρgh). No 6º andar, em comparação ao 2º andar, existe uma coluna de líquido de altura menor sobre o ponto de consumo. Logo, a pressão sobre a torneira será menor.
-
Questão 2
Um turista, ao contratar um passeio turístico para visitar corais no fundo do mar a uma profundidade mais elevada, nota que, conforme submerge, sente maior pressão em seus tímpanos e em seu tórax. Considerando a diferença de densidade entre o ar e a água, pode-se afirmar que, em relação à pressão sentida pelo turista,
A) não existe qualquer diferença na pressão sentida pelo turista conforme ele mergulha mais ao fundo, pois a densidade da água é constante.
B) as forças que a água exerce no mergulhador diminuem a pressão sofrida por ele enquanto imerso.
C) conforme o turista mergulha mais a fundo, a coluna de pressão sobre ele aumenta, em comparação com o ar dentro de seu corpo.
D) conforme o turista mergulha mais a fundo, a densidade da água se torna cada vez maior.
Alternativa C.
Conforme o turista emerge, além da coluna de pressão atmosférica, irá atuar sobre ele uma coluna de pressão da água. Conforme a profundidade aumenta, essa coluna, se torna mais intensa e pode causar desconforto em pessoas inexperientes com a prática do mergulho em águas mais profundas.
-
Questão 3
Em um salão de venda de carros usados, um promotor de venda resolve valorizar um dos veículos disponíveis citando que o sistema de freio usa um mecanismo hidráulico de pressão para sua ativação. Curioso, um cliente pergunta ao promotor se ele saberia explicar como funciona. Prontamente, o promotor responde corretamente que:
A) o pedal do freio, ao ser pressionado, tem sua força transmitida de forma igual para os freios na roda.
B) o pedal do freio, ao ser pressionado, tem sua força transmitida de forma amplificada para os freios na roda.
C) o pedal do freio, ao ser pressionado, tem sua força transmitida de forma reduzida para os freios na roda.
D) o pedal do freio, ao ser pressionado, tem sua força anulada para garantir a ação dos freios na roda.
Alternativa B.
De acordo com o princípio de Pascal (F1/A1 = F2/A2), a pressão aplicada tanto no freio como no pedal é a mesma. Porém, como a pressão é uma grandeza que depende da força aplicada sobre uma área, haverá uma relação de proporcionalidade inversa entre essas duas grandezas. Assim, como a área do pedal é maior do que a área transversal do tubo que transmite a pressão, a força aplicada no freio será maior do que no pedal.
-
Questão 4
Uma professora de Física, disposta a demonstrar a ação da pressão de uma coluna de pressão de água, utiliza um cilindro que tem 2 metros de altura com dois furos: em relação à base, o primeiro a 0,5 m de altura e o segundo a 1,5 m de altura. Ao preencher o cilindro com água e abrir simultaneamente os dois furos, que possuem áreas iguais, a professora irá demonstrar que:
A) não sairá água de nenhum dos furos devido ao equilíbrio hidrostático na coluna de pressão.
B) a água terá um alcance horizontal maior ao sair do furo mais baixo por conta da maior velocidade devida à coluna de pressão.
C) a água terá um alcance horizontal maior ao sair do furo mais alto por conta da maior velocidade devida à energia potencial acumulada.
D) a água terá o mesmo alcance horizontal maior ao sair dos dois furos por conta de a pressão ser a mesma em cada um deles.
Alternativa B.
O furo mais próximo do chão possui sobre si uma coluna de pressão maior, o que garante uma velocidade de vazão maior, de acordo com a equação de Torricelli (\(v= \sqrt{2gh}\)). Como o alcance depende diretamente da velocidade, o furo mais baixo atingirá uma distância horizontal maior.
-
Questão 5
Um agricultor utiliza, em seu cultivo, um sistema de irrigação baseado no gotejamento que depende da pressão no tubo principal. Se a tubulação for muito extensa, com um pequeno diâmetro, pode ocorrer uma queda significativa de pressão nos furos mais distantes. Conceitualmente, isso ocorre porque:
A) o atrito ao longo do tubo diminui a pressão estática, tornando os últimos furos com vazão mais fracas.
B) a pressão hidrostática se mantém constante, já que a água se encontra em repouso.
C) a pressão aumenta ao longo do tubo, já que a velocidade de escoamento diminui.
D) a pressão apenas depende da densidade da água.
Alternativa A.
Como a água está em movimento, o atrito com as paredes irá provocar a perda de pressão. Quanto menor o diâmetro, maior a ação do atrito no escoamento.
-
Questão 6
Um enfermeiro, ao usar uma seringa, puxa o êmbolo para extrair o conteúdo de uma amostra de um recipiente. Notando a surpresa do paciente, o enfermeiro explica que,
A) ao puxar o êmbolo, a pressão interna da seringa aumenta.
B) ao puxar o êmbolo, a pressão interna da seringa diminui.
C) ao puxar o êmbolo, a pressão interna ainda fica constante.
D) ao puxar o êmbolo, a densidade do líquido diminui.
Alternativa B.
Quando puxa o êmbolo, o volume interno da seringa aumentará, e, com isso, a pressão interna, por consequência, irá diminuir. A diferença de pressão fará com que o líquido escoe para o interior da seringa.
-
Questão 7
Um professor, para demonstrar o princípio de Pascal, utiliza duas colunas de líquido ligadas por um vaso comunicante. Os cilindros possuem diâmetros diferentes. Ao pressionar um êmbolo sobre o cilindro de área maior,
A) o êmbolo no cilindro de área menor aplicará a mesma força.
B) o êmbolo no cilindro de área menor aplicará uma força menor.
C) o êmbolo no cilindro de área menor aplicará uma força maior.
D) o êmbolo no cilindro de área menor se manterá estático.
Alternativa C.
De acordo com o princípio de Pascal, dois cilindros unidos por um vaso comunicante possuirão a mesma pressão em ambos os êmbolos. Logo, o aumento da pressão em um acarretará o aumento da pressão no outro. Porém, como a pressão depende da força aplicada sobre uma área, as duas grandezas são inversamente proporcionais.
-
Questão 8
Um tanque de água possui um fundo completamente irregular, com diversos pontos em alturas diferentes. Em relação à pressão hidrostática no fundo,
A) a pressão em cada ponto é a mesma, independentemente da sua altura.
B) a pressão em cada ponto só depende do volume do tanque.
C) a pressão em cada ponto depende apenas da largura horizontal do tanque.
D) a pressão em cada ponto dependerá de sua altura em relação ao ponto mais baixo.
Alternativa D.
A pressão de uma coluna hidrostática, em um líquido em repouso, depende de sua altura, não importando o formato do tanque ou o seu volume.
-
Questão 9
(PUC) A figura mostra um macaco hidráulico, contendo óleo, e constituído de dois êmbolos de áreas A1=1,2 x 101 mm2 e A2 = 1,2 x 104 mm2. Sobre o êmbolo de área A2, é colocado, em repouso, um bloco de massa 6,0 x 102 kg.
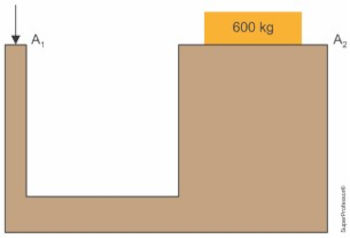
Determine o valor, em newtons, da força aplicada no êmbolo de área A1 para que essa estrutura permaneça em equilíbrio.
Considere g = 10 m/s2
A) 6,0
B) 10
C) 12
D) 5,0
Alternativa A.
Aplicando o princípio de Pascal, obtemos:
\(P_1 = P_2 \rightarrow \frac{F_1}{A_1} = \frac{F_2}{A_2}\\ \frac{F_1}{12 \cdot 10^1} = \frac{600 \cdot 10}{1,2 \cdot 10^4}\\ \therefore F_1 = 6N\)
-
Questão 10
(FGV) A figura mostra três recipientes, L, M e N, que contêm água, sendo que a altura da água no recipiente L é h, no recipiente M é 2h e no recipiente N é 3h. A área da base do recipiente L é igual ao dobro da área da base do recipiente M e ao triplo da área da base do recipiente N.
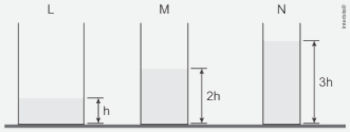
Comparando-se as pressões PL, PM e PN exercidas pela água nas bases dos recipientes L, M e N, respectivamente, tem-se
A) PL = 4PM = 9PN
B) PL = 2PM = 3PN
C) PL = PM = PN
D) \(P_L=\frac{1}{2}P_M=\frac{1}{3}P_N\)
E) \(P_L=\frac{1}{4}P_M=\frac{1}{9}P_N\)
Alternativa D.
Pela lei de Stevin, as pressões exercidas pela água nas bases dos recipientes são:
\(\begin{cases} P_L = \rho g h \\ P_M = \rho g \cdot 2h = 2\rho g h \\ P_N = \rho g \cdot 3h = 3\rho g h \end{cases} \Rightarrow P_L = \frac{1}{2} P_M = \frac{1}{3} P_N \)
-
Questão 11
(EEAR) Em um sistema de vasos comunicantes, são colocados dois líquidos imiscíveis, água com densidade de 1,0 g/cm3 e óleo com densidade de 0,85 g/cm3. Após os líquidos atingirem o equilíbrio hidrostático, observa-se, numa das extremidades do vaso, um dos líquidos isolados, que fica a 20 cm acima do nível de separação, conforme pode ser observado na figura.

Determine o valor de x, em cm, que corresponde à altura acima do nível de separação e identifique o líquido que atinge a altura x.
A) 8,5; óleo
B) 8,5; água
C) 17,0; óleo
D) 17,0; água
Alternativa D.
Como a água possui maior densidade, ela é o líquido que fica mais abaixo e atinge a altura x. Igualando as pressões na altura da linha tracejada, temos:
\(P_{\text{óleo}} = P_{\text{água}} \)
\(P_0 + \rho_{\text{óleo}} \cdot g \cdot h_{\text{óleo}} = P_0 + \rho_{\text{água}} \cdot g \cdot h_{\text{água}} \Rightarrow \rho_{\text{óleo}} \cdot h_{\text{óleo}} = \rho_{\text{água}} \cdot h_{\text{água}}\)
\(0{,}85 \cdot 20 = 1 \cdot x\)
\(\therefore x = 17\ \text{cm}\)
-
Questão 12
(EFOMM) O tipo de manômetro mais simples é o de tubo aberto, conforme a figura abaixo.
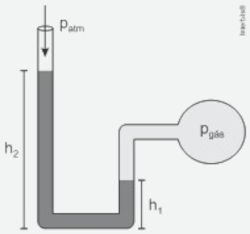
Uma das extremidades do tubo está conectada ao recipiente que contém um gás a uma pressão pgás, e a outra extremidade está aberta para a atmosfera. O líquido dentro do tubo em forma de U é o mercúrio, cuja densidade é 13,6 X 103 kg/m3. Considere as alturas h1 = 5,0 cm e h2 = 8,0 cm. Qual é o valor da pressão manométrica do gás em pascal?
Dado: g = 10 m/s2
A) 4,01 X 103
B) 4,08 X 103
C) 40,87 X 102
D) 4,9 X 104
E) 48,2 X 102
Alternativa B.
Sabendo que a pressão manométrica do gás é dada por pm = patm,int pelo teorema de Stevin, temos que:
\(p_m = \rho_{\text{Hg}} \cdot g \cdot (h_2 - h_1)\)
\(p_m = 13{,}6 \cdot 10^3 \cdot 10 \cdot (8 - 5) \cdot 10^{-2} \\\)
\(\therefore p_m = 4{,}08 \cdot 10^3\ \text{Pa}\)