Exercícios sobre combinação simples
Esta lista de exercícios testará seus conhecimentos sobre combinação simples, um dos agrupamentos estudados na análise combinatória.
Publicado por: Raul Rodrigues de OliveiraQuestões
-
Questão 1
O número de combinações possíveis de 20 elementos tomados de 2 em 2 é igual a:
A) 80
B) 120
C) 190
D) 250
E) 380
Alternativa C
Calculando a combinação, temos que:
\(C_{20,2}=\frac{20!}{2!(20-2)!}\)
\(C_{20,2}=\frac{20!}{2!18!}\)
\(C_{20,2}=\frac{20\cdot19\cdot18!}{2\cdot1\cdot18!}\)
\(C_{20,2}=\frac{20\cdot19}{2}\)
\(C_{20,2}=10\cdot19\)
\(C_{20,2}=190\)
-
Questão 2
Durante os experimentos sobre genética, Mendel precisou escolher 3 mudas diferentes de ervilha para serem cobaias do mesmo experimento. Sabendo que ele tinha disponível 10 mudas naquele dia, então o número de maneiras distintas que ele poderia escolher as cobaias é igual a:
A) 90
B) 120
C) 160
D 200
E) 240
Alternativa B
Calculando a combinação, temos que:
\(C_{10,3}=\frac{10!}{3!\left(10-3\right)!}\)
\(C_{10,3}=\frac{10!}{3!7!}\)
\(C_{10,3}=\frac{10\cdot9\cdot8\cdot7!}{3!7!}\)
\(C_{10,3}=\frac{10\cdot9\cdot8}{3\cdot2\cdot1}\)
\(C_{10,3}=120\)
-
Questão 3
Durante o campeonato intercolegial, o Colégio Brasil Escola dispunha de 12 atletas, sendo que 2 deles eram goleiros. Sabendo que os demais jogadores jogam em qualquer posição, e que o time é composto por 5 jogadores de linha e 1 goleiro, de quantas maneiras distintas o técnico pode montar o time que disputará a final?
A) 12
B) 63
C) 126
D) 252
E) 504
Alternativa E
Como há 2 goleiros, então restam 10 jogadores de linha, logo, queremos calcular todas as combinações possíveis de 10 elementos tomados de 5 em 5.
\(C_{10,5}=\frac{10!}{5!\left(10-5\right)!}\)
\(C_{10,5}=\frac{10!}{5!5!}\)
\(C_{10,5}=\frac{10\cdot9\cdot8\cdot7\cdot6\cdot5!}{5!5!}\)
\(C_{10,5}=\frac{10\cdot9\cdot8\cdot7\cdot6}{5\cdot4\cdot3\cdot2\cdot1}\)
\(C_{10,5}=\frac{30240}{120}\)
\(C_{10,5}=252\)
Como há 2 possibilidades de goleiro, multiplicaremos a quantidade de times de linha possíveis por 2.
\(252\cdot2=504\ \)
-
Questão 4
No Dia das Crianças, a escola do Heitor decidiu realizar o sorteio de 2 caixas de chocolate entre os 15 estudantes da turma. Cada um deles recebeu um número de 1 até 15, e foram retirados 2 números da urna. O número de duplas possíveis para ganhar esse prêmio é igual a:
A) 105
B) 210
C) 235
D) 260
E) 300
Alternativa A
Calculando a combinação de 15 elementos tomados de 2 em 2, temos que:
\(C_{15,2}=\frac{15!}{2!\left(15-2\right)!}\)
\(C_{15,2}=\frac{15!}{2!13!}\)
\(C_{15,2}=\frac{15\cdot14\cdot13!}{2\cdot1\cdot13!}\)
\(C_{15,2}=\frac{15\cdot14}{2}\)
\(C_{15,2}=15\cdot7\)
\(C_{15,2}=105\)
-
Questão 5
Em uma sala de aula de 3ª série do ensino médio, decidiu-se montar a comissão de formatura composta por 4 estudantes da turma. Sabendo que nessa turma tem 2 alunas, que se chamam Natália e Lara, e que, incluindo as 2, a turma tem 20 estudantes, o número de comissões possíveis em que as referidas alunas estarão presentes é igual a:
A) 102
B) 204
C) 408
D) 816
E) 1632
Alternativa D
Se há 20 estudantes, incluindo Natália e Lara, então escolheremos 3 estudantes entre os 18 restantes, já que 2 lugares da comissão estão ocupados por elas. Calculando as combinações, temos que:
\(C_{18,3}=\frac{18!}{3!\left(18-3\right)!}\)
\(C_{18,3}=\frac{18!}{3!15!}\)
\(C_{18,3}=\frac{18\cdot17\cdot16\cdot15!}{3!15!}\)
\(C_{18,3}=\frac{18\cdot17\cdot16}{3\cdot2\cdot1}\)
\(C_{18,3}=816\)
-
Questão 6
Para aumentar os seus rendimentos, Laiza decidiu vender macarrão na feira. Ela oferece 3 opções de macarrão, além de 15 opções de acompanhamentos, como bacon, queijo, azeitona, calabresa, diferentes molhos, entre outros. Na porção de macarrão, o cliente deve escolher o tipo de massa que ele deseja e até 4 acompanhamentos. Para melhorar o seu marketing, Laiza fez uma placa dizendo aos seus clientes que a sua loja possui mais de 5000 opções de pedidos. Analisando essa placa, podemos afirmar que:
A) a placa não está correta, pois há exatamente 165 pedidos possíveis.
B) a placa não está correta, pois há exatamente 1940 pedidos possíveis.
C) a placa não está correta, pois há exatamente 4095 pedidos possíveis.
D) a placa está correta, pois há exatamente 5820 pedidos possíveis.
E) a placa está correta, pois há exatamente 5823 pedidos possíveis.
Alternativa E
Primeiro calcularemos os pedidos possíveis. Sabemos que o cliente escolherá até 4 dos 15 acompanhamentos possíveis, logo, calcularemos quantos opções temos com 4 ingredientes, 3 ingredientes, 2 ingredientes e 1 ingrediente:
\(C_{15,4}=\frac{15!}{4!11!}=1365\)
\(C_{15,3}=\frac{15!}{3!12!}=455\)
\(C_{15,2}=\frac{15!}{2!13!}=105\)
\(C_{15,1}=\frac{15!}{1!14!}=15\)
Somando, temos que:
\(1365 + 455 + 105 + 15 = 1940\)
Sabemos que há 3 tipos de macarrão, logo, para cada tipo de macarrão, há 1904 combinações possíveis de acompanhamento:
\(1940\cdot3=5820\ \)
Por fim, o cliente pode pedir também somente o macarrão, sem acompanhamento nenhum, logo, podemos acrescentar 3 opções.
\(5820+3=5823\)
Então há 5823 pedidos diferentes que um cliente pode fazer.
-
Questão 7
Trinta e dois cantores se inscreveram em um torneiro de música amador. Na primeira etapa do torneiro, foi sorteado os 4 primeiros cantores, que comporão o grupo 1. Depois disso, foram sorteados do grupo 1 os 2 primeiros cantores, que farão a abertura da competição.
A quantidade total de escolhas possíveis para o grupo 1 e a quantidade total de escolhas dos 2 cantores que farão a abertura da competição pode ser calculada, respectivamente, por:
A) uma combinação e uma permutação
B) uma combinação e um arranjo
C) um arranjo e uma combinação
D) dois arranjos
E) duas combinações
Alternativa E
Note que, na primeira escolha e na segunda escolha, a ordem não é importante. Quando temos agrupamentos em que a ordem não é relevante, então os agrupamentos são combinações.
-
Questão 8
Durante as aulas de Geografia, a professora Kárita decidiu sortear 4 estudantes para passarem um dia no clube com tudo pago. Se nessa turma há 20 alunos, e todos eles possuem a mesma chance de serem sorteados, então o número de resultados possíveis para esse sorteio pode ser calculado por:
A) \(A_{20,4}\)
B) \(20!\)
C) \(P_{20}\)
D) \(C_{20,4}\)
E) \(P_{20}^4\)
Alternativa D
Analisando a situação, podemos perceber que os agrupamentos do sorteio não possuem ordem, pois o agrupamento formado por 4 estudantes em específico será o mesmo, independentemente da ordem em que eles forem sorteados. Quando a ordem não importa, então o agrupamento é uma combinação, sendo assim, calcularemos utilizando C20,4 — combinação de 20 elementos tomados de 4 em 4.
-
Questão 9
(Enem) O tênis é um esporte em que a estratégia de jogo a ser adotada depende, entre outros fatores, de o adversário ser canhoto ou destro. Um clube tem um grupo de 10 tenistas, sendo que 4 são canhotos e 6 são destros. O técnico do clube deseja realizar uma partida de exibição entre dois desses jogadores, porém não poderão ser ambos canhotos.
Qual o número de possibilidades de escolha dos tenistas para a partida de exibição?
A) \( \frac{10!}{2!8!}-\frac{4!}{2!2!}\)
B) \( \frac{10!}{8!}-\frac{4!}{2!}\)
C) \( \frac{10!}{2!8!}-2\)
D) \( \frac{6!}{4!}+4\cdot4\)
E) \( \frac{6!}{4!}+6\cdot4\)
Alternativa A
Calcularemos todas as duplas possíveis e depois vamos subtrair todas as duplas em que ambos são canhotos.
As duplas possíveis são uma combinação de 10 elementos tomados de 2 em 2, e as duplas em que ambos são canhotos são uma combinação de 4 elementos tomados de 2 em 2, logo, temos que:
\(C_{10,2}-C_{4,2}=\frac{10!}{2!8!}-\frac{4!}{2!2!}\)
-
Questão 10
(Enem 2019) Durante suas férias, oito amigos, dos quais dois são canhotos, decidem realizar um torneio de vôlei de praia.
Eles precisam formar quatro duplas para a realização do torneio. Nenhuma dupla pode ser formada por dois jogadores canhotos.
De quantas maneiras diferentes podem ser formadas essas quatro duplas?
A) 69
B) 70
C) 90
D) 104
E) 105
Alternativa C
Primeiro calcularemos a quantidade de duplas possíveis, a primeira dupla é uma combinação de 8 tomados de 2 em 2, a segunda, de 6 tomados de 2 em 2, e assim sucessivamente. É necessário dividir o resultado por 4, já que a ordem em que a dupla sair não faz diferença no torneio.
\(C_{8,2}\cdot C_{6,2}\cdot C_{4,2}\cdot C_{2,2}\ ∶\ 4!\)
Calculando as combinações, temos que:
\(C_{8,2}\cdot C_{6,2}\cdot C_{4,2}\cdot C_{2,2}\ ∶\ 4!\ =\ 105\)
Agora, é necessário calcular todas as combinações em que há uma dupla de canhotos.
\(C_{6,2}\cdot C_{4,2}\cdot C_{2,2}\ ∶\ 3!\ =\ 15\)
Calculando a subtração:
\(105\ -\ 15\ =\ 90\ \)
-
Questão 11
(Enem 2021) Uma pessoa produzirá uma fantasia utilizando como materiais: 2 tipos de tecidos diferentes e 5 tipos distintos de pedras ornamentais. Essa pessoa tem à sua disposição 6 tecidos diferentes e 15 pedras ornamentais distintas. A quantidade de fantasias com materiais diferentes que podem ser produzidas é representada pela expressão:
A) \( \frac{6!}{4!2!}\cdot\frac{15!}{10!5!}\)
B) \( \frac{6!}{4!2!}+\frac{15!}{10!5!}\)
C) \( \frac{6!}{2!}+\frac{15!}{5!}\)
D) \( \frac{6!}{2!}\cdot\frac{15!}{5!}\)
E) \( \frac{21!}{7!14!}\)
Alternativa A
Há duas combinações para serem calculadas, uma calculará o número de maneiras distintas que o tecido pode ser escolhido, uma combinação de 6 elementos tomados de 2 em 2; já a outra é a combinação de 15 elementos tomados de 5 em 5, que nos dá o número de maneiras distintas que as pedras podem ser escolhidas. Dessa forma, temos que:
\(C_{6,4}\cdot C_{15,5}=\frac{6!}{4!2!}\cdot\frac{15!}{10!5!}\)
-
Questão 12
(Enem 2019) Uma empresa confecciona e comercializa um brinquedo formado por uma locomotiva, pintada na cor preta, mais 12 vagões de iguais formato e tamanho, numerados de 1 a 12. Dos 12 vagões, 4 são pintados na cor vermelha, 3 na cor azul, 3 na cor verde e 2 na cor amarela. O trem é montado utilizando-se uma locomotiva e 12 vagões, ordenados crescentemente segundo suas numerações, conforme ilustrado na figura.
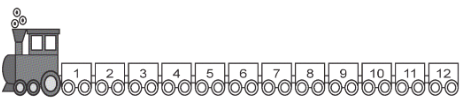
De acordo com as possíveis variações nas colorações dos vagões, a quantidade de trens que podem ser montados, expressa por meio de combinações, é dada por:
A) \(C_{12}^4\times C_{12}^3\times C_{12}^3\times C_{12}^2\)
B) \( C_{12}^4+C_{12}^3+C_5^3+C_2^2\)
C) \( C_{12}^4\times2\times C_8^3\times C_5^2\)
D) \( C_{12}^4+2{\times C}_{12}^3+C_{12}^2\)
E) \( C_{12}^4\times C_8^3\times C_5^3\times C_2^2\)
Alternativa E
Queremos 4 vagões vermelhos: \(C_{12}^4\). Após escolher os vagões vermelhos, queremos 3 vagões azuis: \(C_8^3\). Dos 5 restantes, escolheremos 3 para serem verdes \(C_5^3\). Por fim, os últimos 2 serão amarelos: \(C_2^2\). Pelo princípio multiplicativo, temos que:
\(C_{12}^4\times C_8^3\times C_5^3\times C_2^2\)