Exercícios sobre determinantes
Esta lista de exercícios sobre determinantes testará seus conhecimentos sobre as determinantes de matrizes com questões resolvidas sobre suas principais propriedades.
Publicado por: Raul Rodrigues de OliveiraQuestões
-
Questão 1
O valor do determinante da matriz a seguir é:
\(A=\left[\begin{matrix}4&3\\2&1\\\end{matrix}\right]\)
A) -2
B) -1
C) 0
D) 1
E) 2
Alternativa A
Vamos fazer o cálculo do determinante:
\(detA=4\cdot1-3\cdot2\)
\(detA=4-6\)
\(detA=-2\)
-
Questão 2
Qual deve ser o valor de x na matriz para que seu determinante seja igual a 5?
\(B=\left[\begin{matrix}x+1&4\\x&3\\\end{matrix}\right]\)
A) -2
B) -1
C) 0
D) 1
E) 2
Alternativa A
\(detB=\left(x+1\right)\cdot3-4\cdot x\)
\(detB=3x+3-4x\)
\(detB=-x+3\)
Sabendo que esse determinante é igual a 5, então temos que:
− x + 3 = 5
− x = 5 − 3
− x = 2 (−1)
x = − 2
-
Questão 3
Analise a matriz a seguir:
\(A=\left(\begin{matrix}1&4&1\\2&2&-1\\3&0&1\\\end{matrix}\right)\)
O determinante dessa matriz é igual a:
A) -12
B) -16
C) -24
D) 15
E) 32
Alternativa C
Calculando o determinante da matriz, temos que:
\(detA=\left|\begin{matrix}1&4&1\\2&2&-1\\3&0&1\\\end{matrix}\right|\begin{matrix}1&4\\2&2\\3&0\\\end{matrix}\)
\(detA=1\cdot2\cdot1+4\cdot\left(-1\right)\cdot3+1\cdot2\cdot0-1\cdot2\cdot3-1\cdot\left(-1\right)\cdot0-4\cdot2\cdot1\)
\(detA=2-12+0-6-0-8\)
\(detA=-24\)
-
Questão 4
Dada as matrizes \(A=\left[\begin{matrix}6&-6\\1&4\\\end{matrix}\right]\) e \(B=\left[\begin{matrix}2&8\\-2&4\\\end{matrix}\right]\), então a razão entre o determinante da matriz A e o da matriz B é igual a:
A) 2/3
B) 3/2
C) 4/5
D) 5/4
Alternativa D
Calculando os determinantes, temos que:
\(det\left(A\right)=6\cdot4-\left(-6\right)\cdot1=24+6=30\)
\(det\left(B\right)=2\cdot4-8\cdot\left(-2\right)=8+16=24\)
Então, a razão entre det(A) e det(B) é igual a:
\(\frac{{30}^{:6}}{{24}_{:6}}=\frac{5}{4}\)
-
Questão 5
Analisando a matriz \(A=\left[\begin{matrix}4&x+3\\x-4&-3\\\end{matrix}\right]\), o menor valor de x que faz com que det(A) = 0 é:
A) -2
B) -1
C) 0
D) 1
E) 2
Alternativa C
Calculando o determinante, temos que:
\(det\left(A\right)=4\cdot\left(-3\right)-\left(x+3\right)\cdot\left(x-4\right)\)
\(det\left(A\right)=-12-\left[x^2-4x+3x-12\right]\)
\(det\left(A\right)=-12-\left[x^2-x-12\right]\)
\(det\left(A\right)=-12-x^2+x+12\)
\(det\left(A\right)={-x}^2+x\)
Queremos que:
\(-x^2+x=0\)
Então temos que:
\(x\left(-x+1\right)=0\)
x = 0 ou \(-x+1=0\)
Resolvendo a segunda, temos que:
\(-x=-1\)
\(x=1\)
Então as soluções são x = 0 e x = 1. Como queremos a menor delas, temos que x = 0.
-
Questão 6
Seja A a matriz \(A=\left[\begin{matrix}5&2\\3&0\\\end{matrix}\right]eB a matrizB=\left[\begin{matrix}8&5\\2&1\\\end{matrix}\right]\), então o determinante da matriz det(A+B) é igual a:
A) -10
B) -8
C) -6
D) -4
E) -2
Alternativa B
Sabemos que:
det(A+B) = detA + detB
Então temos que:
\(detA=5\cdot0-3\cdot2=0-6=-6\)
\(detB=8\cdot1-5\cdot2=8-10=-2\)
Dessa forma:
det (A + B) = - 6 + ( - 2) = - 8
-
Questão 7
Dada a matriz \(A=\left(\begin{matrix}2&3&1\\4&6&1\\x&y&1\\\end{matrix}\right)\), sabemos que o determinante dela igualado a zero nos dá a equação da reta que passa pelos pontos os pontos (2,3) (4,6). Então essa equação será:
A) 3x + 2y = 0
B) -3x + 2y = 0
C) -2x + y =0
D) 2x – y = 0
E) x – 3y = 0
Alternativa B
Calculando o determinante, temos que:
\(de\left(A\right)=2\cdot6\cdot1+3\cdot1\cdot x+1\cdot4\cdot y-1\cdot6\cdot x-2\cdot1\cdot y-3\cdot4\cdot1\)
\(det\left(A\right)=12+3x+4y-6x-2y-12\)
\(det\left(A\right)=-3x+2y\)
Assim, a equação da reta será:
\(-3x+2y=0\)
-
Questão 8
Sobre a matriz \(A=\left|\begin{matrix}a&b&c\\d&0&f\\2a&2b&2c\\\end{matrix}\right|\), podemos afirmar que:
A) O seu determinante é 0, pois a linha 1 e a linha 3 são múltiplas.
B) O seu determinante é 0, pois o termo central da matriz é 0.
C) O seu determinante pode ser diferente de 0, dependendo dos valores de a, b, c.
E) O seu determinante é igual a 1, pois o produto da diagonal principal é 0.
Alternativa A
Quando uma linha da matriz é multiplicada de outra, o determinante é igual a 0, fato esse que acontece com as linhas 1 e 3.
-
Questão 9
(UEL) A soma dos determinantes indicados a seguir é igual a zero
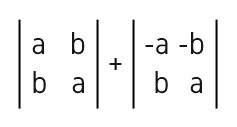
A) quaisquer que sejam os valores reais de a e de b.
B) se e somente se a = b.
C) se e somente se a = -b.
D) se e somente se a = 0.
E) se e somente se a = b = 1.
Alternativa A
Calculando os determinantes, temos que:
\(a\cdot a-b\cdot b\pm a\cdot a-\left(-b\right)\cdot b=0\)
\(a^2-b^2-a^2+b^2=0\)
\(0=0\)
Note que, independentemente do valor de a e de b, essa soma dos determinantes sempre será igual a 0.
-
Questão 10
(PM ES – AOCP). Para saber o custo total (em reais) na produção de x uniformes para um grupo de soldados, primeiramente substitui-se cada elemento x, da matriz a seguir, pela quantidade de uniformes que se quer produzir, e calcula-se o determinante dessa matriz, obtendo-se, assim, o custo total na produção destes x uniformes é igual ao valor do determinante.
\(\left|\begin{matrix}x&1&0\\0&-x&100\\0&-1&1\\\end{matrix}\right|\)
Dessa forma, para se produzir 70 uniformes para um grupo de soldados, o custo total nessa produção será de
A) R$ 4100.
B) R$ 3500.
C) R$ 3100.
D) R$ 2500.
E) R$ 2100.
Alternativa E
Calculando o determinante da matriz, temos que:
\(det=x\cdot\left(-x\right)\cdot1+1\cdot100\cdot0+0\cdot0\cdot\left(-1\right)–0⋅-x⋅0–-1⋅100⋅x–1⋅0⋅1\)
\(det=-x^2+100x\)
Como x = 70, temos que:
\(det=-{70}^2+100\cdot70\)
\(det=-4900+7000\)
\(det=2100\)
-
Questão 11
(Uesp) Se o determinante da matriz \(\left[\begin{matrix}2&1&0\\k&k&k\\1&2&-2\\\end{matrix}\right]\) é igual a 10, então o determinante da matriz \(\left[\begin{matrix}2&1&0\\k+4&k+3&k-1\\1&2&-2\\\end{matrix}\right]\) é igual a:
A) 7
B) 8
C) 9
D) 10
E) 11
Alternativa C
Calculando o determinante da primeira matriz:
\(A=\left[\begin{matrix}2&1&0\\k&k&k\\1&2&-2\\\end{matrix}\right]\)
Temos que:
\(det\left(A\right)=2\cdot k\cdot\left(-2\right)+1\cdot k\cdot1+0\cdot k\cdot2-0\cdot k\cdot1-2\cdot k\cdot2-1\cdot k\cdot\left(-2\right)\)
\(det\left(A\right)=-4k+k+0-0-4k+2k\)
\(det\left(A\right)=-5k\)
Como det(A) = 10, temos que:
\(-5k=10\)
\(k=\frac{10}{-5}\)
\(k=-2\)
Sabendo que k = 2, então agora é possível calcular o determinante da segunda matriz, substituindo k por 2.
\(B=\left[\begin{matrix}2&1&0\\k+4&k+3&k-1\\1&2&-2\\\end{matrix}\right]\)
\(B=\left[-\begin{matrix}2&1&0\\2+4&-2+3&-2-1\\1&2&-2\\\end{matrix}\right]\)
\(B=\left[\begin{matrix}2&1&0\\2&1&-3\\1&2&-2\\\end{matrix}\right]\)
Calculando det(B), temos que:
\(det\left(B\right)=2\cdot1\cdot\left(-2\right)+1\cdot\left(-3\right)\cdot1+0\cdot2\cdot2-0\cdot1\cdot1-2\cdot\left(-3\right)\cdot2-1\cdot2\cdot\left(-2\right)\)
\(det\left(B\right)=-4-3+0+0+12+4\)
\(det\left(B\right)=9\)
-
Questão 12
(IBADE 2018) Considere as matrizes A e B, quadradas de ordem 2, com detA = 10 e detB = 2. Então o valor de det[(4.A).(3.B)] é igual:
A) \( 2^6\cdot3^2\cdot5^3\)
B) \( 2^4\cdot3^3\cdot5\)
C) \( 2^6\cdot3^2\cdot5^2\)
D) \( 2^6\cdot3^2\cdot5\)
E) \( 2^6\cdot3^4\cdot5\)
Alternativa D
Analisando os determinantes, temos que:
\(det\left[\left(4\cdot A\right)\cdot\left(3\cdot B\right)\right]=det\left(4A\right)\cdot det\left(3B\right)\)
Sabendo que a matriz é de ordem 2, temos que:
\(det\left[\left(4\cdot A\right)\cdot\left(3\cdot B\right)\right]=4^2det\left(A\right)\cdot3^2det\left(B\right)\)
\(det\left[\left(4\cdot A\right)\cdot\left(3\cdot B\right)\right]=4^2\cdot10\cdot3^2\cdot2\)
\(det\left[\left(4\cdot A\right)\cdot\left(3\cdot B\right)\right]=2^4\cdot2\cdot5\cdot3^2\cdot2\)
\(det\left[\left(4\cdot A\right)\cdot\left(3\cdot B\right)\right]=2^6\cdot3^2\cdot5\)