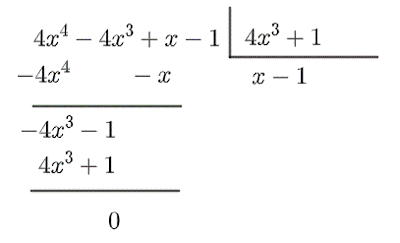Exercícios sobre divisão de polinômios
Esta lista de exercícios composta por questões resolvidas sobre divisão de polinômios te auxiliará nos seus estudos sobre o assunto.
Publicado por: Raul Rodrigues de OliveiraQuestões
-
Questão 1
Seja Q(x) a divisão do polinômio 2x³ - 4x² + 2x pelo polinômio 2x, o valor de Q(1) é:
A) - 1
B) 0
C) 1
D) 2
E) 3
Alternativa B
Para calcular o valor de Q(1), primeiramente calcularemos a divisão do polinômio:
(2x³ - 4x² + 2x) : (2x)
Dividindo cada termo pelo monômio, encontraremos o seguinte polinômio:
Q(x) = x² - 2x + 1
Substituindo x = 1, temos que:
Q(1) = 1² - 2 ⋅ 1 + 1 = 1 - 2 + 1 = 0
-
Questão 2
Seja \(P(x)=4x^4-4x^3+x-1\), ao realizar a sua divisão pelo polinômio \(D(x)=4x^3+1\) encontramos como resto:
A) x - 1
B) x + 1
C) x + 2
D) 0
E) 1
-
Questão 3
Ao ser divido pelo polinômio x - 2, o polinômio \(x^4-2x^3+2x+1 \) deixa resto igual a:
A) 1
B) 2
C) 3
D) 4
E) 5
Alternativa E
Aplicando o teorema de D’Alembert, temos que:
x - 2 = 0
x = 2
Substituindo x = 2 no dividendo, é possível encontrar o seu resto na divisão dele por x - 2:
\(x^4-2x^3+2x+1\)
\(2^4-2⋅ 2^3+2⋅2+1\)
\(16- 16 + 4 + 1\)
\(5 \)
-
Questão 4
O polinômio P(x) foi reescrito como o produto entre os polinômios Q(x) e D(x). Sabendo que P(x) = 15x² + 11x + 2 e que D(x) = 3x + 1, o polinômio Q(x) será igual a:
A) 5x
B) 5x + 2
C) 5x - 2
D) 2x + 5
E) 2x - 5
Alternativa B
Realizando a divisão:
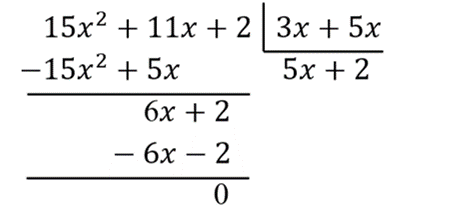
Então, o quociente Q(x) = 5x + 2.
-
Questão 5
Dados os polinômios P(x) = \(6x^4-x^3+3x^2-x+1\) e \(D(x)=2x^2+x-3\), se Q(x) for o quociente da divisão entre eles, o valor de Q(2) é:
A) 9
B) 10
C) 12
D) 15
E) 18
Alternativa D
Primeiramente, calcularemos a divisão:
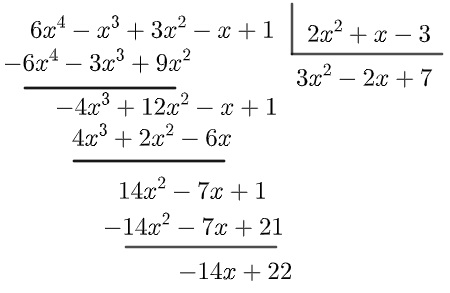
Agora sabemos que Q(x) = 3x² - 2x + 7. Calculando Q(2):
\(Q(2)=3⋅2^2-2⋅2+7\)
\(Q(2)=3⋅4-4 +7\)
\(Q(2)=12-4 + 7\)
\(Q(2)=8+7\)
\(Q(2)=15\)
-
Questão 6
Considerando os polinômios P(x) = 2x³ - x² - 8x + 1 e Q(x) = 8x² + 2x - 3, o valor P(2) : Q(0) é:
A) 1
B) 0
C) - 1
D) 2
E) - 2
Alternativa A
Calculando o valor numérico de cada polinômio:
\(P(2)=2⋅2^3-2^2-8⋅2+1\)
\(P(2)=2⋅8-4-16+1\)
\(P(2)=16-4-16+1\)
\(P(2)=-3\)
\(Q(0)=8⋅0^2+2⋅0-3\)
\(Q(0)=-3\)
Então P(2) : Q(0) = - 3 : (- 3) = 1.
-
Questão 7
Dado o polinômio P(x) = \(x^3-kx^2+9x\), o valor de k que faz com que esse polinômio seja divisível por pelo polinômio x - 3 é:
A) - 3
B) - 4
C) - 5
D) - 6
E) - 7
Alternativa D
Utilizando o teorema de D’Alembert:
x - 3 = 0
x = 3
Para que essa divisão seja exata, temos que P(3) = 0.
Substituindo x = 3 no polinômio P(x) e o igualando a 0, temos que:
\(P(3)=3^3-k⋅3^2+9⋅3\)
\(0=27-9k+27\)
\(54=-9k\)
\(k=\frac{54}{-9}\)
\(k=-6\)
-
Questão 8
Simplifique a expressão:
\(\frac{3a^2 b^3-9a^3 b^2+6ab}{3ab}\)
Ao realizar a divisão, encontramos o polinômio:
A) ab - 3a² + 2
B) ab² + a²b + 3
C) ab² - 3a²b +2
D) a²b³ - 3a³b² +2ab
E) 3ª²b³ - 9ª³b² +2
Alternativa C.
Dividiremos cada termo do polinômio por 3ab:
3a²b³ : 3ab = ab
- 9a³b² : 3ab = - 3a²b
6ab : 3ab = 2
Assim, a divisão resultará no polinômio ab - 3a²b + 2
-
Questão 9
Sobre a divisão de polinômios, podemos afirmar que:
I. O grau do polinômio que representa o resto é sempre igual ou maior que o grau do polinômio que representa o divisor.
II. Quando o resto da divisão de P(x) por D(x) é 0, dizemos que o polinômio P(x) é divisível por D(x).
Marque a alternativa correta:
A) Somente a afirmativa I é verdadeira.
B) Somente a afirmativa II é verdadeira.
C) As duas afirmativas são verdadeiras.
D) As duas afirmativas são falsas.
Alternativa B
I. O grau do polinômio que representa o resto é sempre igual ou maior que o grau do polinômio que representa o divisor. (Falso)
O grau do resto é sempre igual ou menor que o grau do divisor.
II. Quando o resto da divisão de P(x) por D(x) é 0, dizemos que o polinômio P(x) é divisível por D(x). (Verdadeiro)
Quando a divisão não deixa resto, P(x) é divisível por D(x).
-
Questão 10
Considere o polinômio P(x) = x³ - x² + 3x - 3 e o polinômio Q(x) = x - 1. Podemos afirmar que:
A) P(x) é divisível por Q(x).
B) P(x) deixa resto 1 na divisão por Q(x).
C) P(x) deixa resto 2 na divisão por Q(x).
D) P(x) deixa resto 3 na divisão por Q(x).
E) P(x) deixa resto 5 na divisão por Q(x).
Alternativa A
Calculando o resto da divisão usando o teorema de D’Alembert:
x - 1 = 0
x = 1
Calculando P(1):
P(1) = 1³ - 1² + 3 ⋅ 1 - 3
P(1) = 1 - 1 + 3 - 3
P(1) = 0
Como o resto é 0, então P(x) é divisível por Q(x).
-
Questão 11
Existe um polinômio P(x) tal que P(x) : D(x) tem como resto R(x) = 11 e quociente Q(x) = 2x - 7.
Se o divisor D(x) é igual a x + 1, então P(x) será o polinômio:
A) 2x² - 5x + 4
B) 3x² - 4x + 7
C) 2x² + 4
D) 3x² - 5x + 11
E) 3x² - 8x + 11
Alternativa A
Sabemos que:
P(x) = Q(x) ⋅ D(x) + R(x)
Então, temos que:
P(x) = (2x - 7) (x + 1) + 11
P(x) = 2x2 + 2x - 7x - 7 + 11
P(x) = 2x2 - 5x + 4
-
Questão 12
(UEG) Dividindo o polinômio P(x) = 3x³ + 5x² - 12x + 5 pelo polinômio D(x) = x² + 2x - 5 obtêm-se, respectivamente, o quociente Q(x) e o resto R(x) iguais a:
A) Q(x) = 3x + 1 e R(x) = 0
B) Q(x) = x + 3 e R(x) = 4x + 2
C) Q(x) = x - 3 e R(x) = 4x - 2
D) Q(x) = 3x - 1 e R(x) = 5x
Alternativa D
Calculando a divisão:
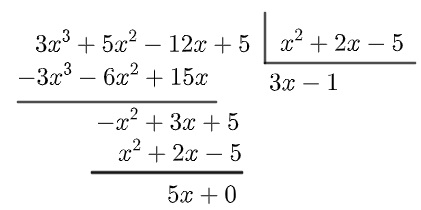
O quociente é Q(x) = 3x – 1, e o resto é R(x) = 5x.