Exercícios sobre expressão algébrica
Esta lista de exercícios sobre expressão algébrica te auxiliará nos estudos sobre os principais conceitos envolvendo o tema.
Publicado por: Raul Rodrigues de OliveiraQuestões
-
Questão 1
O valor numérico da expressão ax + a² – a²x + ax² – 2x³ + 3a³, para a = 2 e x = 1, é:
A) 12
B) 19
C) 20
D) 23
E) 26
Alternativa E
Calculando o valor para a = 2 e x = 1:
\(ax + a^2 – a^2x + ax^2 – 2x^3 + 3a^3\)
\(2\cdot 1 + 2^2 - 2^2\cdot 1 + 2\cdot 1^2 - 2\cdot 1^3 + 3\cdot2^3\)
\(2\cdot1 +4-4\cdot1+2\cdot1-2\cdot1+3\cdot8\)
\(2+4-4+2-2+24\)
\(26\)
-
Questão 2
Durante a resolução de exercícios sobre expressões algébricas, o professor pediu para que os alunos realizassem a simplificação da expressão 8(3 – 5x) + 4(3x – 6). Se a simplificação for feita matematicamente, o polinômio encontrado será:
A) 28x + 24
B) -12
C) -14x + 12
D) -28x
E) 52x + 48
-
Questão 3
Um quadrado possui a medida dos seus lados iguais a (x + 3). Sabendo que a área de um quadrado é igual ao quadrado do seu lado, então a área do quadrado em questão é igual a:
A) x² + 3
B) x³ + 9
C) x² + 6x
D) x² + 6x + 9
E) x² + 6x + 3
Alternativa D
Para achar a área do quadrado, calcularemos o valor de (x + 3)²:
(x + 3)² = (x + 3)(x + 3)
(x + 3)² = x² + 3x + 3x + 9
(x + 3)² = x² + 6x + 9
-
Questão 4
Dadas as expressões algébricas Ax² – By² + x + 2y + 6 e 5x² + 4y² + Cx + D + 1, marque a alternativa que contém o valor de A + B + C + D, sabendo que eles são polinômios semelhantes.
A) 3
B) 4
C) 5
D) 6
E) 7
Alternativa E
Como eles são polinômios semelhantes, temos que:
Ax² – By² + x + 2y + 6 = 5x² + 4y² + Cx + D + 1
Pelo primeiro termo, temos que:
A = 5
Agora igualando o segundo termo:
-B = 4
B = -4
Igualando o terceiro termo:
C = 1
Igualando os termos independentes:
D + 1 = 6
D = 6 – 1
D = 5
Assim, temos que:
A + B + C + D = 5 – 4 + 1 + 5 = 11 – 4 = 7
-
Questão 5
Dadas as expressões algébricas a seguir, marque aquela que pode ser classificada como um binômio:
A) ax²
B) 3a + 2x
C) 2ax
D) 2x + 3y + z
E) 2
Alternativa B
Uma expressão algébrica é classificada como binômio quando ela possui exatamente dois termos, que correspondem, nesse caso, a: 3a + 2x.
-
Questão 6
Dadas as expressões algébricas A: 2x + 3y + 4 e B: 5x – 3y, então o valor de A + B será:
A) 11xy
B) 7x + y + 4
C) 7x + 4
D) 5x – 4
E) 7x – y
Alternativa C
Realizando a soma dos termos semelhantes, temos que:
A + B = 2x + 3y + 4 + 5x – 3y
A + B = 7x – 0y + 4
A + B = 7x + 4
-
Questão 7
Analisando a expressão \(\frac{\sqrt{x+y}}{\sqrt y-\sqrt x}\), sabendo que x = 9 e y = 16, então o valor dessa expressão é:
A) 2
B) 3
C) 4
D) 5
E) 6
Alternativa D
Substituindo x = 9 e y = 16, temos que:
\(\frac{\sqrt{9+16}}{\sqrt{16}-\sqrt9}=\frac{\sqrt{25}}{4-3}=\frac{5}{1}=5\)
-
Questão 8
Analise o retângulo a seguir:
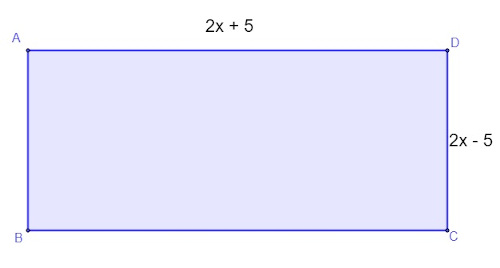
Sabendo que a área do retângulo é o produto dos seus lados, então a expressão algébrica que representa a área do retângulo acima é:
A) 2x² + 5
B) 4x² + 25
C) 4x² – 25
D) 4x² – 10x + 25
E) 4x² + 20x – 25
Alternativa C
Calculando a multiplicação entre a base e a altura do retângulo, temos que:
(2x + 5) (2x – 5) = 4x² – 10x + 10x – 25
(2x + 5) (2x – 5) = 4x² – 25
Então a área A desse retângulo pode ser expressa por:
A = 4x² – 25
-
Questão 9
(Enem - 2019) Uma empresa tem diversos funcionários. Um deles é o gerente, que recebe R$ 1000 por semana. Os outros funcionários são diaristas. Cada um deles trabalha 2 dias por semana, recebendo R$ 80 por dia trabalhado. Chamando de X a quantidade total de funcionários da empresa, a quantia Y, em reais, que esaa empresa gasta semanalmente para pagar seus funcionários é expressa por:
A) Y = 80X + 920
B) Y = 80X + 1000
C) Y = 80X + 1080
D) Y = 160X + 840
E) Y = 160X + 1000
Alternativa D
Sabemos que X é o número de funcionários total da empresa. Tirando o gerente da conta, o número de diaristas é (X – 1).
Sabemos que o valor recebido, por semana, por diarista é de:
\(2\cdot80=160\)
Então temos que:
Y = (X – 1) ∙ 160 + 1000
Y = 160X + 840
-
Questão 10
(Enem) O prefeito de uma cidade deseja construir uma rodovia para dar acesso a outro município. Para isso, foi aberta uma licitação na qual concorreram duas empresas. A primeira cobrou R$ 100 000 por km construído (n), acrescido de um valor fixo de R$ 350 000, enquanto a segunda cobrou R$ 120 000 por km construído (n), acrescido de um valor fixo de R$ 150 000. As duas empresas apresentam o mesmo padrão de qualidade dos serviços prestados, mas apenas uma delas poderá ser contratada. Do ponto de vista econômico, qual equação possibilitaria encontrar a extensão da rodovia que tornaria indiferente para a prefeitura escolher qualquer uma das propostas apresentadas?
A) 100n + 350 = 120n + 150
B) 100n + 150 = 120n + 350
C) 100(n + 350) = 120(n + 150)
D) 100(n + 350 000) = 120(n + 150 000)
E) 350(n + 100 000) = 150(n + 120 000)
Alternativa A
Montando a equação, temos que:
100 000n + 350 000 = 120 000n + 150 000
Simplificando a expressão, encontraremos a equação:
100 n + 350 = 120 n + 150
-
Questão 11
(Enem - 2018) Uma empresa deseja iniciar uma campanha publicitária divulgando uma promoção para seus possíveis consumidores. Para esse tipo de campanha, os meios mais viáveis são a distribuição de panfletos na rua e os anúncios na rádio local. Considera-se que a população alcançada pela distribuição de panfletos seja igual à quantidade de panfletos distribuídos, enquanto a alcançada por um anúncio na rádio seja igual à quantidade de ouvintes desse anúncio. O custo de cada anúncio na rádio é de R$ 120, e a estimativa é de que seja ouvido por 1500 pessoas. Já a produção e a distribuição dos panfletos custam R$ 180 cada 1000 unidades. Considerando que cada pessoa será alcançada por um único desses meios de divulgação, a empresa pretende investir em ambas as mídias. Considere X e Y os valores (em real) gastos em anúncios na rádio e com panfletos respectivamente. O número de pessoas alcançadas pela campanha será dado pela expressão:
A) \(\frac{50X}{4}+\frac{50Y}{9}\)
B) \(\frac{50X}{9}+\frac{50Y}{4}\)
C) \(\ \frac{4X}{50}+\frac{4Y}{50}\)
D) \(\frac{50}{4X}+\frac{50}{9Y}\)
E) \(\frac{50}{9X}+\frac{50Y}{4Y}\)
Alternativa A
Sabemos que, para cada R$ 120 gastos, são atingidas 1500 pessoas.
Calculando a razão para o rádio:
\(\frac{1500}{120}=\frac{50}{4}\ pessoas\ atingidas\ por\ reais\)
Já para os panfletos, temos que, a cada 180 reais, são atingidas 1000 pessoas:
\(\frac{1000}{180}=\frac{50}{9}\ pessoas\ atingidas\ por\ reais\)
Então o alcance é dado pela expressão:
\(A=\ \frac{50X}{4}+\frac{50Y}{9}\)
-
Questão 12
(IBFC) As expressões algébricas que contêm números e letras são utilizadas para representar situações no cotidiano. Para tornar mais simples o cálculo de áreas, verificamos os monômios, polinômios e termos semelhantes. Veja a Figura 03 - Área Algébrica:
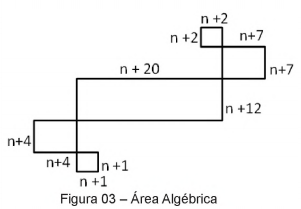
Qual expressão algébrica representa o perímetro total da Figura 03 - Área Algébrica? Assinale a alternativa correta.
A) 20n + 120
B) 10n + 60
C) 15n + 6
D) 5n + 7
Alternativa A
Calculando a soma dos lados, temos que:
\(2\left(n+1\right)+2\left(n+1\right)+2\left(n+4\right)+2\left(n+4\right)+2\left(n+20\right)+2\left(n+12\right)+2\left(n+7\right)+2\left(n+7\right)+2\left(n+2\right)+2\left(n+2\right)\)
\(4\left(n+1\right)+4\left(n+4\right)+2\left(n+20\right)+2\left(n+12\right)+4\left(n+7\right)+4\left(n+2\right)\)
\(4n+4+4n+16+2n+40+2n+24+4n+28+4n+8\)
\(20n+120\)