Exercícios sobre fatorial
Resolva esta lista de exercícios sobre fatorial de um número natural e teste seus conhecimentos sobre esse assunto da análise combinatória.
Publicado por: Raul Rodrigues de OliveiraQuestões
-
Questão 1
Uma fila é composta por 7 pessoas; de quantas maneiras diferentes essas pessoas podem se organizar nessa fila?
A) 5040
B) 2520
C) 1440
D) 720
E) 504
Alternativa A.
Para saber a quantidade de filas possíveis, basta calcular o valor de 7!:
P7 = 7!
p7 = 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 5040
-
Questão 2
Ao realizar a simplificação da expressão \(\frac{10!}{8!} \), o valor encontrado é:
A) 90
B) 720
C) 90!
D) 10
E) 360
Alternativa A.
Para simplificar, temos que:
\(\frac{10 \ \cdot \ 9 \ \cdot \ 8!}{8!} = 10 \cdot 9 = 90 \)
-
Questão 3
Qual é o valor de 0!?
A) Indeterminado
B) 0
C) 1
D) 2
E) 10
Alternativa C.
Por definição, 0! = 1.
-
Questão 4
Marque a alternativa que contém a forma correta de calcular n!.
A) n! = n + (n – 1) + (n – 2) + ... + 3 + 2 + 1.
B) n! = n ⋅ (n – 1) ⋅ (n – 2) ⋅ ... ⋅ 3 ⋅ 2 ⋅ 1.
C) n! = n – (n – 1) – (n – 2) – ... – 3 – 2 – 1.
D) n! = n + (n – 1) – (n – 2) + ... – 3 + 2 – 1.
E) n! = n ⋅ (n – 1) ⋅ (n – 2) ⋅ ... ⋅ 3 ⋅ 2 ⋅ 1 ⋅ 0.
Alternativa B.
Por definição, o fatorial de n é o produto do número por todos os antecessores até 1, ou seja:
n! = n ⋅ (n – 1) ⋅ (n – 2) ⋅ ... ⋅ 3 ⋅ 2 ⋅ 1
-
Questão 5
Analise as afirmativas a seguir:
I. 2! + 3! = 5!
II. 4! – 3! = 2!
III. 5! : 4! = 5
Marque a alternativa correta:
A) Somente a afirmativa I é verdadeira.
B) Somente a afirmativa II é verdadeira.
C) Somente a afirmativa III é verdadeira.
D) Todas as afirmativas são verdadeiras.
E) Todas as afirmativas são falsas.Alternativa C.
I. 2! + 3! = 5! (incorreta)
2! = 2 × 1 = 2
3! = 3 × 2 × 1 = 6
5! = 5 × 4 × 3 × 2 × 1 = 120
Então, temos:
2! + 3! = 2 + 6 = 8
5! = 120
Portanto, 2! + 3! ≠ 5!; a afirmativa I é falsa.
II. 4! – 3! = 2! (incorreta)
4! = 4 × 3 × 2 × 1 = 24
3! = 3 × 2 × 1 = 6
2! = 2 × 1 = 2
Agora, vamos calcular:
4! – 3! = 24 – 6 = 18
2! = 2
Então, 4! – 3! ≠ 2!; a afirmativa II é falsa.
III. 5! : 4! = 5 (correta)
5! = 5 × 4 × 3 × 2 × 1 = 120
4! = 4 × 3 × 2 × 1 = 24
Agora, vamos dividir:
5! : 4! = 120 : 24 = 5
Portanto 5! : 4! = 5; a afirmativa III é verdadeira.
-
Questão 6
Qual é o valor de x na equação (3x - 2)! = 5040?
A) 4
B) 5
C) 3
D) 6
E) 7Alternativa C.
O número n, cujo n! = 5040, é n = 7, pois 7! = 5040; então temos que:
(3x - 2)! = 7!
3x - 2=7
3x = 7 + 2
3x = 9
\(x = \frac {9}{3}\)
x = 3
-
Questão 7
Uma escola possui 8 professores de matemática, que devem tirar um intervalo de 15 minutos antes do horário de almoço. O intervalo é organizado de modo que 7 professores fiquem disponíveis para atender aos alunos ao mesmo tempo, sendo que apenas um professor tira o intervalo de cada vez. O coordenador determina a ordem dos intervalos. Qual é o número de maneiras distintas que o coordenador pode definir a ordem dos intervalos?
A) 8!
B) 7!
C) 8! : 7!
D) 7! ⋅ 2
E) 8! − 1
Alternativa B.
Sabemos que se 8 professores estão disponíveis, mas um deles tira o intervalo de cada vez, então a quantidade de maneiras de organizar os intervalos é dada pela permutação dos 7 professores que estarão de serviço. Ou seja, o número de maneiras de organizar o intervalo é dado por 7!.
-
Questão 8
Calcule o valor da expressão 4! + 3!.
A) 30
B) 27
C) 12
D) 24
E) 36
Alternativa A.
Para calcular o valor da expressão é necessário calcular cada um dos fatoriais:
4! = 4 ⋅ 3 ⋅ 2 ⋅ 1 = 24
3! = 3 ⋅ 2 ⋅ 1 = 6
Somando 4! + 3!:
24 + 6 = 30
-
Questão 9
(Enem) Um cliente de uma videolocadora tem o hábito de alugar dois filmes por vez. Quando os devolve sempre pega outros dois filmes e assim sucessivamente. Ele soube que a videolocadora recebeu alguns lançamentos, sendo 8 filmes de ação, 5 de comédia e 3 de drama e, por isso, estabeleceu uma estratégia para ver todos esses 16 lançamentos. Inicialmente alugará, em cada vez, um filme de ação e um de comédia. Quando se esgotarem as possibilidades de comédia, o cliente alugará um filme de ação e um de drama, até que todos os lançamentos sejam vistos e sem que nenhum filme seja repetido.
De quantas formas distintas a estratégia desse cliente poderá ser posta em prática?
A) 20 ⋅ 8! + (3!)2
B) 8! ⋅ 5! ⋅ 3!
C) \(\frac{8! \ \cdot \ 5! \ \cdot \ 3!}{2^8} \)
D) \(\frac{8! \ \cdot \ 5! \ \cdot \ 3!}{2^2} \)
E) \(\frac{16!}{2^8} \)
Alternativa B.
Para esse cliente alugar os 16 filmes lançamentos, serão feitas 8 locações, já que ele aluga 2 por vez.
O número de maneiras que ele pode escolher o filme de ação é dado por 8!, já o filme de comédia é 5! e o filme de drama é 3!, então ele pode alugar o filme de:
\(8! ⋅5! ⋅3! \ maneiras\)
-
Questão 10
(Enem) Nos livros Harry Potter, um anagrama do nome do personagem “TOM MARVOLO RIDDLE" gerou a frase "I AM LORD VOLDEMORT”.
Suponha que Harry quisesse formar todos os anagramas da frase “I AM POTTER”, de tal forma que as vogais e consoantes aparecessem sempre intercaladas, e sem considerar o espaçamento entre as letras.
Nessas condições, o número de anagramas formados é dado por
A) 9!
B) 4! 5!
C) 2 × 4! 5!
D) \(\frac{9!}{2!} \)
E) \(\frac{4! \ \cdot \ 5!}{2} \)
Alternativa E.
Podemos observar que existem 4 vogais, A, E, I, O. Além disso, há 5 consoantes, M, P, T, T, R.
Como são 4 vogais e sem repetição, o número de maneiras distintas que podemos ordenar as vogais é igual ao fatorial de 4, ou seja, 4!; já nas consoantes temos uma repetição \(\frac{5!}{2} \).
Então o número de maneiras distintas é:
\(4! \cdot \frac{5!}{2} = \frac{4! \ 5!}{2} \)
-
Questão 11
(Enem) Uma família composta por sete pessoas adultas, após decidir o itinerário de sua viagem, consultou o site de uma empresa aérea e constatou que o voo para a data escolhida estava quase lotado. Na figura, disponibilizada pelo site, as poltronas ocupadas estão marcadas com X, e as únicas poltronas disponíveis são as mostradas em branco.
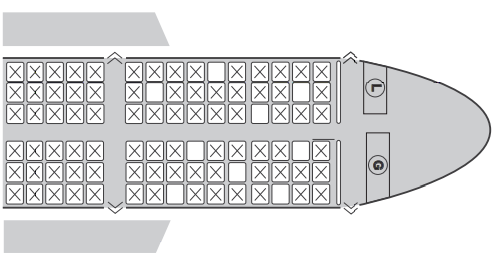
O número de formas distintas de se acomodar a família nesse voo é calculado por:
A) \(\frac {9!}{2}\)
B) \(\frac {9!}{7! \ 2!}\)
C) 7!
D) \(\frac {5!}{2!} ⋅ 4!\)
E) \(\frac {5!}{4!} ⋅ \frac {4!}{3!}\)
Alternativa A.
Caso fossem 9 poltronas e 9 pessoas, o número de maneiras distintas que essas pessoas se sentariam poderia ser calculado por 9!; entretanto sabemos que há 2 vazias, então vamos dividir pela permutação entre elas, já que as duas poltronas ficarão vazias sem importar a ordem, ou seja:
\(N = \frac {9!}{2!}\)
-
Questão 12
Em uma competição de matemática, 8 alunos participaram e foram classificados do 1º ao 8º lugar. De quantas maneiras diferentes é possível organizar esses 8 alunos na competição?
A) 8!
B) 7!
C) 82
D) 8 ⋅ 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3
E) 8 ⋅ 7 ⋅ 6
Alternativa A.
Para contar de quantas maneiras possíveis esses 8 alunos podem se classificar basta calcular a permutação de 8 elementos, ou seja:
P8 = 8!