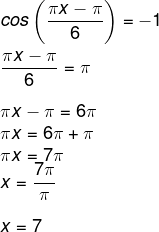Exercícios sobre funções trigonométricas
Esta lista de exercícios possui questões resolvidas sobre as principais funções trigonométricas e vai te ajudar nos seus estudos sobre o tema.
Publicado por: Raul Rodrigues de OliveiraQuestões
-
Questão 1
Dada a função f(x) = sen x + 3, o valor numérico da função para x = 3π/2 é:
A) 0.
B) 1.
C) 2.
D) 3.
E) 4.
Alternativa C.
Para encontrar o valor numérico da função, basta substituir o valor que desejamos no lugar de x:
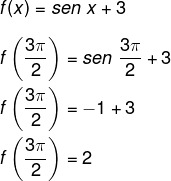
-
Questão 2
Conhecendo a função f(x) = 4 cos (2x) + 1, podemos afirmar que a imagem da função é igual a:
A) [– 2, 2].
B) [– 3, 5].
C) [ – 1, 1].
D) [ – 4, 8].
E) ] – ∞ , ∞[.
Alternativa B.
Sabemos que o valor de cosseno é 1 e o menor é -1, então:
Limite superior do intervalo:
Seja cos (2x) = 1:
f(x) = 4 · 1 +1
f(x) = 4 + 1
f(x) = 5
Limite inferior do intervalo:
cos(2x) = -1:
f(x) = 4 · ( – 1) + 1
f(x) = – 4 + 1
f(x) = – 3
A imagem da função é o intervalo [– 3, 5].
-
Questão 3
Dada a função trigonométrica a seguir:
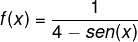
Podemos afirmar que o menor valor que f(x) pode assumir é:
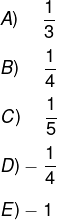
Alternativa C.
Em uma fração, quanto maior o denominador, menor é o valor da fração. Então, o valor que deixa o denominador ser o maior número possível é sen(x) = – 1.
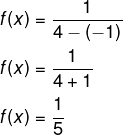
-
Questão 4
Analise o gráfico da função trigonométrica a seguir:
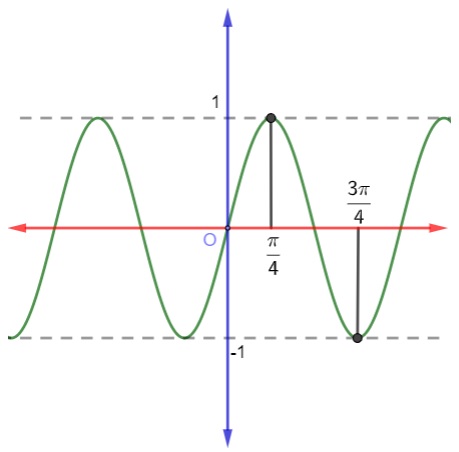
A lei de formação que descreve a função demonstrada no gráfico é:
A) f(x) = sen (x).
B) f(x) = cos (x).
C) f(x) = sen (2x).
D) f(x) = cos (2x).
E) f(x) = 2tg(x).
Alternativa C.
Analisando o gráfico, sabemos que o seu comportamento é senoide, pois ele passa pelo ponto (0,0) e sen(0) = 0.
Note também que, quando x = π/4, f(x) = 1.
Seja f(x) = sen(ax), encontraremos o valor de a, lembrando que o ângulo cujo sen(x) = 1 é o ângulo π/2:
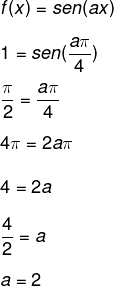
Então, a função é f(x) = sen(2x).
-
Questão 5
Dada a função f(x) = 1 + 2cos(x), seja x um ângulo do primeiro quadrante, então o valor de x que faz com que f(x) = 2 é:
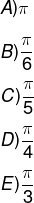
Alternativa E.

O arco cujo cosseno é igual a ½ que pertence ao primeiro quadrante é o ângulo de 60º, ou seja, π/3.
-
Questão 6
Sobre as funções trigonométricas, julgue as afirmativas as seguir:
I → A função seno (f(x) = sen(x)) e a função cosseno (g(x) = cos(x)) possuem imagem no intervalo [–1,1].
II → A função tangente (tg(x)) possui imagem entre [2, – 2].
III → A função seno é uma função periódica.
Marque a alternativa correta:
A) Somente a afirmativa I é falsa.
B) Somente a afirmativa II é falsa.
C) Somente a afirmativa III é falsa.
D) Todas as afirmativas são verdadeiras.
Alternativa B.
I → Verdadeira. Devido ao ciclo trigonométrico, a função seno e a função cosseno possuem valores sempre entre -1 e 1.
II → Falsa. A função tangente não é limitada, e a sua imagem é o conjunto dos números reais.
III → Verdadeira. A função seno possui período igual a 2π.
-
Questão 7
Dada a função f(x) = sen²(x) + 2cos(x), o valor numérico da função para x = π/4 é:
A) 0,5 + √2.
B) 1 + √2.
C) 4.
D) 4 – √2.
E) 0,5 + √3.
Alternativa A.
Substituindo o valor de x pelo valor dado, temos que:
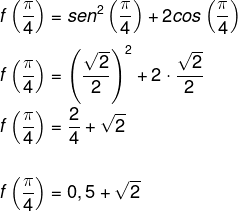
-
Questão 8
Analise o gráfico da função trigonométrica a seguir:
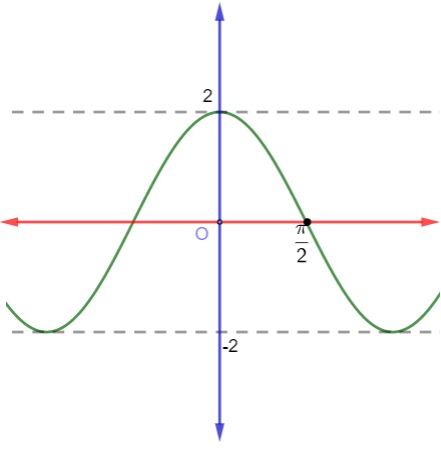
A lei de formação que descreve essa função é:
A) f(x) = sen (2x).
B) f(x) = cos (2x).
C) f(x) = 2sen (x).
D) f(x) = 2cos (x).
E) f(x) = 2tg(x).
Alternativa D.
Note que o máximo e o mínimo da função são 2 e -2. Perceba que a função passa pelo ponto (0,2). Para que isso aconteça, essa função tem que ser uma função cosseno multiplicada por 2, pois, se fosse a função seno, o gráfico passaria pelo ponto (0,0).
Perceba, por fim, que π/2 é zero da função e sabemos que cos (π/2) = 0.
Então, a função é f(x) = 2cos(x).
-
Questão 9
(Enem 2011) Um satélite de telecomunicações, t minutos após ter atingido sua órbita, está a r quilômetros de distância do centro da Terra. Quando r assume seus valores máximo e mínimo, diz-se que o satélite atingiu o apogeu e o perigeu, respectivamente. Suponha que, para esse satélite, o valor de r em função de t seja dado por:
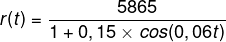
Um cientista monitora o movimento desse satélite para controlar o seu afastamento do centro da Terra. Para isso, ele precisa calcular a soma dos valores de r, no apogeu e no perigeu, representada por S.
O cientista deveria concluir que, periodicamente, S atinge o valor de:
A) 12 765 km
B) 12 000 km
C) 11 730 km
D) 10 965 km
E) 5 865 km
Alternativa B.
Queremos a distância entre o maior valor e o menor valor da função. Para encontrar o máximo e o mínimo da função, substituiremos cosseno por 1 e por – 1.
cos(0,6t) = 1

Agora faremos cos(0,6t) = – 1.

A diferença entre esses valores é igual a:
6900 +5100 = 12000
-
Questão 10
(UFSM 2007) Uma gráfica que confeccionou material de campanha determina o custo unitário de um de seus produtos, em reais, de acordo com a lei C(t) = 200 + 120 . sen (π . t/2), com t medido em horas de trabalho. Assim, os custos máximos e mínimo desse produto são:
A) 320 e 200
B) 200 e 120
C) 200 e 80
D) 320 e 80
E) 120 e 80
Alternativa D.
Sabemos que a função seno possui maior valor quando seno é igual a 1 e menor quando seno é igual a – 1.
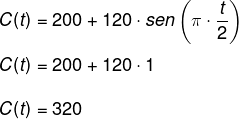
O maior valor é 320. Agora calcularemos o menor valor:
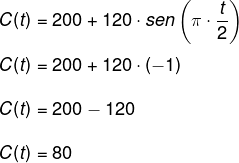
-
Questão 11
Sobre a função f(x) = sen (x), julgue as afirmativas a seguir:
I → Essa função é uma função trigonométrica e periódica.
II → No domínio [0, 2π], existem dois zeros para a função.
III → A imagem da função no domínio [0,2π] é o intervalo [0, 1].
Marque a alternativa correta:
A) Somente a afirmativa I é falsa.
B) Somente a afirmativa II é falsa.
C) Somente a afirmativa III é falsa.
D) Todas as afirmativas são verdadeiras.
Alternativa C.
I → Verdadeira. A função é uma função trigonométrica, pois possui uma razão trigonométrica em função do ângulo. Além disso, a função seno é periódica.
II → Verdadeira. Nesse intervalo, o seno de 0º e de π é igual a zero.
III → Falsa. Substituindo os extremos, temos que sen(0) = 0 e sen(2π) = 1.
-
Questão 12
(Enem) Segundo o Instituto Brasileiro de Geografia e Estatística (IBGE), produtos sazonais são aqueles que apresentam ciclos bem definidos de produção, consumo e preço. Resumidamente, existem épocas do ano em que a sua disponibilidade nos mercados varejistas ora é escassa, com preços elevados, ora é abundante, com preços mais baixos, o que ocorre no mês de produção máxima da safra.
A partir de uma série histórica, observou-se que o preço P, em reais, do quilograma de um certo produto sazonal pode ser descrito pela função

onde x representa o mês do ano, sendo x = 1 associado ao mês de janeiro, x = 2 ao mês de fevereiro, e assim sucessivamente, até x = 12 associado ao mês de dezembro.
Na safra, o mês de produção máxima desse produto é:
A) janeiro.
B) abril.
C) junho.
D) julho.
E) outubro.
Alternativa D.
A safra tem seu valor máximo quando o preço é o mínimo possível. Para isso, o menor valor que o cosseno pode assumir é -1, então: