Exercícios sobre inequações modulares
Estes exercícios sobre inequações modulares requerem a aplicação das propriedades operatórias de módulo, bem como as aplicações gerais de inequação.
Publicado por: Amanda Gonçalves RibeiroQuestões
-
Questão 1
Resolva a inequação modular |3x + 5| < 20.
Vamos remover o módulo da inequação |3x + 5| < 20 para resolvê-la:
|3x + 5| < 20
– 20 < 3x + 5 < 20
– 20 – 5 < 3x < 20 – 5
– 25 < 3x < 15
– 25 < x < 15
3 3
– 25 < x < 5
3Portanto, o conjunto solução é
. -
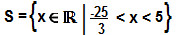Questão 2
Resolva a inequação modular 2 ≤ |2x + 1| ≤ 10 no conjunto dos reais.
Para resolver a inequação modular 2 ≤ |2x + 1| ≤ 10, é indicado separá-la em duas inequações modulares distintas:
(i) |2x + 1| ≤ 10
(ii) 2 ≤ |2x + 1|Vamos agora resolver a inequação (i) |2x + 1| ≤ 10:
|2x + 1| ≤ 10
– 10 ≤ 2x + 1 ≤ 10
– 10 – 1 ≤ 2x ≤ 10 – 1
– 11 ≤ 2x ≤ 9
– 11 ≤ x ≤ 9
2 2Já com a inequação (ii) |2x + 1| ≥ 2, temos:
2x + 1≥ 2 ou 2x + 1≤ - 2
Resolvendo o primeiro caso da inequação (ii)
2x + 1≥ 2
2x ≥ 2 – 1
2x ≥ 1
x≥ ½Resolvendo o segundo caso da inequação (ii)
2x + 1≤ - 2
2x ≤ -2 – 1
2x ≤ -3
x ≤ -3/2Logo a solução da inequação II é:
x≥ ½ ou x ≤ -3/2
Por fim, montamos o quadro de resolução:
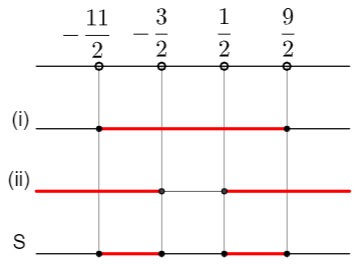
Quadro de resolução da questão 2A solução que compreende todos os x reais é
.
-
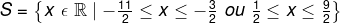
Questão 3
(EEM – SP) Determine os valores reais de x para os quais 1 < |x – 1| < 2:
Para resolver a inequação 1 < |x – 1| < 2, vamos desmembrá-la em duas inequações modulares:
(i) 1 < |x – 1| ou |x – 1| > 1
(ii) |x – 1| < 2Resolvendo a inequação (i) |x – 1| > 1, temos:
|x – 1| > 1
– 1 > x – 1 > 1
– 1 + 1 > x > 1 + 1
0 > x > 2Já com a inequação (ii) |x – 1| < 2, temos:
|x – 1| < 2
– 2 < x – 1 < 2
– 2 + 1 < x < 2 + 1
– 1 < x < 3Por fim, montamos o quadro de resolução:
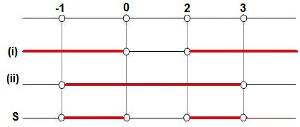
Quadro de resolução da questão 3A solução é
. -
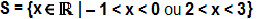Questão 4
(Fuvest) Resolva a inequação x.|x| > x
A propriedade básica de módulo garante que
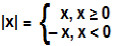. Sendo assim, ao resolver a equação, consideramos os dois casos.1° caso: x ≥ 0
x . x > x
x² > x
x² – x > 0
x.(x – 1) > 0
x' = 0
x'' = 12° caso: x < 0
x . (– x) > x
– x² > x
– x² – x > 0
x² + x < 0
x.(x + 1) < 0
x' = 0
x'' = – 1Vamos verificar a solução para os dois casos:
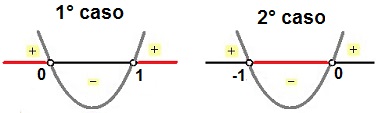
Soluções da questão 4Observe que a solução do 1° caso é x < 0 ou x > 1, já a do 2º caso é – 1 < x < 0. Sendo assim, o conjunto solução é
.
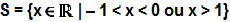