Exercícios sobre matriz simétrica
Teste seus conhecimentos por meio desta lista de exercícios sobre matriz simétrica, a matriz cuja sua transposta é ela mesma.
Publicado por: Raul Rodrigues de OliveiraQuestões
-
Questão 1
Sabendo que a matriz A é simétrica, determine o valor de x.
\(A=\left[\begin{matrix}2&x\\8&7\\\end{matrix}\right]\)
A) 2
B) 8
C) 7
D) -2
E) -7
Alternativa B.
Observe que o enunciado afirma que a matriz é simétrica, logo os elementos a12 e a21 devem ser iguais. Na figura abaixo isso é claro, e podemos concluir que x = 8.
\(A=\left[\begin{matrix}2&\color{red}{x}\\\color{red}{8}&7\\\end{matrix}\right]=\left[\begin{matrix}2&\color{red}{a_{12}}\\\color{red}{a_{12}}&7\\\end{matrix}\right]\)
-
Questão 2
Determine o valor de x e y sabendo que a matriz M é simétrica.
\(M=\left(\begin{matrix}3&x-2&9\\8&4&7\\9&y+2&5\\\end{matrix}\right)\)
A) x = 8 e y = 7
B) x = 6 e y = 9
C) x = 10 e y = 9
D) x = 10 e y = 5
E) x = 5 e y = 7
Alternativa D.
Como o enunciado nos traz que a matriz é uma matriz simétrica, primeiro analisaremos 4 termos dessa matriz em específico:
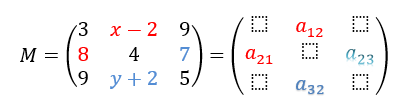
Analisando a matriz, temos que \(\color{red}{\begin{cases} a_{21}=8 \quad \\ a_{12}=x-2& \quad \end{cases}} \) e \( \color{blue}{\begin{cases} a_{32}=y+2 \quad \\ a_{23}=7& \quad \end{cases}} \)
Sabemos que M é matriz simétrica, então a12 = a21 e a32 = a23. Sendo assim, temos que:
\(\color{red}{x-2=8}\)
\(\color{red}{x=8+2}\)
\(\color{red}{x=10}\)
Calculando o valor de y, temos que:
\(\color{blue}{y+2=7}\)
\(\color{blue}{y=7-2}\)
\(\color{blue}{y=5}\)
Então temos que x = 10 e y = 5.
-
Questão 3
Analise as afirmações abaixo e marque a alternativa correta.
I. Toda matriz simétrica é de ordem 2x2.
II. Toda matriz identidade é simétrica.
III. Toda matriz nula é uma matriz simétrica.
A) Apenas o item I é falso.
B) Todos os itens são verdadeiros.
C) Somente os itens I e II são verdadeiros.
D) Temos apenas um item verdadeiro.
E) Todos os itens são falsos.
Alternativa D.
I. Toda matriz simétrica é de ordem 2x2. (falso)
Existem matrizes simétricas de qualquer ordem.
II. Toda matriz identidade é simétrica. (verdadeiro)
Como os elementos fora da diagonal principal são iguais a zero, não há possibilidade para ter \(a_{ij}\neq a_{ji}\).
III. Toda matriz nula é uma matriz simétrica. (falso)
Existem matrizes nulas que não são quadradas, condição necessária para serem simétricas.
-
Questão 4
Considere que a matriz A é simétrica, de ordem 2x2, e obedece à lei de formação:
\(a = \begin{cases} a_{ij}=sen\left(i\pi\right),\ se\ i=1\ \quad \\ a_{ij}=\cos{\left(i\pi\right)},\ se\ i\neq1\ e\ i=j & \quad \end{cases}\)
Determine a matriz B que satisfaz a equação matricial A+B = 0:
A) \(\left(\begin{matrix}1&0\\1&0\\\end{matrix}\right)\)
B) \(\left(\begin{matrix}1&0\\0&1\\\end{matrix}\right)\)
C) \(\left(\begin{matrix}1&0\\0&-1\\\end{matrix}\right)\)
D) \(\left(\begin{matrix}0&0\\0&-1\\\end{matrix}\right)\)
E) \(\left(\begin{matrix}0&0\\0&1\\\end{matrix}\right)\)
Alternativa D.
Vamos montar a matriz genérica com base nas informações do enunciado.
\(A = \left(\begin{matrix}a_{11}&a_{12}\\a_{21}&a_{22}\\\end{matrix}\right)\)
\(a_{11}=sen\left(1\cdot\pi\right)=0\)
\(a_{12}=sen\left(1\cdot\pi\right)=0\)
a21 = 0 (da definição de matriz simétrica, pois a12 = a 21)
\(a_{22}=\cos{\left(2\cdot\pi\right)}=1\)
\(A = \left(\begin{matrix}0&0\\0&1\\\end{matrix}\right)\)
Pelo sistema de equação matricial, temos que B = -A:
\(B = \left(\begin{matrix}0&0\\0&-1\\\end{matrix}\right)\)
-
Questão 5
Determine o valor de a e b sabendo que a matriz A é simétrica.
\(A=\left(\begin{matrix}6&a-b&9\\4&4&6\\9&a+b&9\\\end{matrix}\right)\)
A) a = 4 e b = 7
B) a = 5 e b = 1
C) a = 1 e b = 6
D) a = 3 e b = 5
E) a = 5 e b = 7
Alternativa B.
Analisaremos os termos em destaque:
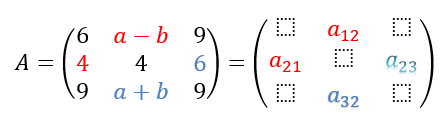
Temos que: \( \color{red}{\begin{cases} a_{21}=4 \quad \\ a_{12}=a-b& \quad \end{cases}}\)e \( \color{blue}{\begin{cases} a_{32}=a+b \quad \\ a_{23}=6& \quad \end{cases}} \)
Ao afirmar que A é matriz simétrica, concluímos que a12=a21 e a32=a23. Sendo assim, temos que:
\( \begin{cases} \color{red}{a-b=4} \quad \\ \color{blue}{a+b=6} & \quad \end{cases}\)
Efetuando a soma das duas linhas:
\(2a=\ 10\)
\(a=\frac{10}{2}\)
\(a=5\)
Logo a=5.
Substituindo esse valor na segunda linha do sistema:
\(a+b=6\)
\(5+b=6\)
\(b=1\)
-
Questão 6
Sabendo que a matriz simétrica N de ordem 2x2 obedece à lei de formação \(a = \begin{cases} a_{12}=3\ \quad \\ a_{ij}=2,\ se\ i=j & \quad \end{cases}\), podemos afirmar que N é:
A) \(\left(\begin{matrix}3&2\\2&3\\\end{matrix}\right)\)
B) \( \left(\begin{matrix}2&2\\3&3\\\end{matrix}\right)\)
C) \( \left(\begin{matrix}2&3\\3&2\\\end{matrix}\right)\)
D) \( \left(\begin{matrix}3&3\\2&2\\\end{matrix}\right)\)
E) \( \left(\begin{matrix}3&2\\3&2\\\end{matrix}\right)\)
Alternativa C.
Vamos montar a matriz genérica com base nas informações do enunciado.
\(N = \left(\begin{matrix}a_{11}&a_{12}\\a_{21}&a_{22}\\\end{matrix}\right)\)
\(a_{11}=2\)
\(a_{22}=2\)
\(a_{12}=3\)
Como a matriz N é simétrica, temos que \(a_{12}=a_{21}=3\).
\(N = \left(\begin{matrix}2&3\\3&2\\\end{matrix}\right)\)
-
Questão 7
Sendo \(N=\left(\begin{matrix}2&3\\-1&2\\\end{matrix}\right)\), \(M=\left(\begin{matrix}7&8\\8&2\\\end{matrix}\right) \) e \(P=\left(\begin{matrix}5&-1\\7&5\\\end{matrix}\right)\) matrizes de ordem 2x2, marque a alternativa verdadeira:
A) N é uma matriz simétrica.
B) M é uma matriz transposta de N.
C) M é matriz simétrica.
D) P é matriz simétrica.
E) N é matriz nula.
Alternativa C.
A alternativa A é falsa, pois caso a matriz N fosse simétrica, os elementos -1 e 3 deveriam ser iguais.
A alternativa B é falsa. As matrizes M e N possuem elementos distintos. Numa matriz transposta o que muda é a ordem dos elementos e não seus valores.
A alternativa C é verdadeira. Os elementos \(a_{12}=a_{21}=8\).
A alternativa D é falsa, pois caso a matriz N fosse simétrica, os elementos -1 e 7 deveriam ser iguais.
A alternativa E é falsa, pois a matriz possui elementos diferentes de zero.
-
Questão 8
\(A=\left(\begin{matrix}7&y\\x&y\\\end{matrix}\right) \) e \(B=\left(\begin{matrix}7&x\\y&2\\\end{matrix}\right)\) são matrizes de ordem 2x2. Sabendo que a matriz B é igual à matriz A e supondo que a matriz A seja matriz simétrica, determine os valores de x e y:
A) x = 7 e y = 2
B) x = 7 e y = 7
C) x = 2 e y = 2
D) x = 2 e y = 7
E) x = 1 e y = 6
Alternativa C.
Pela definição de matriz simétrica, temos que \(A=\left(\begin{matrix}7&\color{red}{y}\\\color{blue}{x}&\color{red}{y}\\\end{matrix}\right)=\left(\begin{matrix}7&\color{blue}{x}\\y&\color{red}{y}\\\end{matrix}\right)=\left(\begin{matrix}7&{x}\\y&\color{red}{2}\\\end{matrix}\right)\). Assim, concluímos que x = y = 2.
-
Questão 9
\(A=\left(\begin{matrix}6&8&9\\x&4&y\\9&6&9\\\end{matrix}\right)\) é uma matriz simétrica. Determine a soma de todos os elementos da matriz oposta de A.
A) 65
B) -65
C) -51
D) 51
E) 34
Alternativa B.
Pela definição de matriz simétrica, temos que:
\(A=\left(\begin{matrix}6&\color{red}{8}&9\\\color{red}{x}&4&y\\9&6&9\\\end{matrix}\right)=\left(\begin{matrix}6&x&9\\8&4&\color{red}{6}\\9&\color{red}{y}&9\\\end{matrix}\right)\)
A partir disso, concluímos que x = 8 e y = 6. Somando os termos dessa matriz e multiplicando por -1, obtemos \(-\left(6+8+9+8+4+6+9+6+9\right)=\color{red}{-65}.\).
-
Questão 10
Sejam X e Y matrizes 2x2 satisfazendo a expressão X∙Y+Y∙X=0. Sabendo que X é matriz simétrica e Y é igual à transposta da matriz X, podemos afirmar que:
A) O determinante de X é 1.
B) O determinante de Y é 1.
C) X é matriz identidade.
D) Y é matriz identidade.
E) X e Y são matrizes nulas.
Alternativa E.
Do fato de a matriz X ser simétrica temos X = Y, logo temos que \(X^2+X^2=2X^2=0\).
Escrevendo esse produto de forma genérica:
\(2\left(\begin{matrix}a&b\\b&c\\\end{matrix}\right)\left(\begin{matrix}a&b\\b&c\\\end{matrix}\right)=2\left(\begin{matrix}a^2+b^2&ab+bc\\ab+b^2&b^2+c^2\\\end{matrix}\right)=\left(\begin{matrix}0&0\\0&0\\\end{matrix}\right)\)
Do resultado acima concluímos que a = 0, e b = 0, e c = 0.
Logo, as matrizes X e Y são matrizes nulas.
-
Questão 11
Sobre a definição de matriz simétrica, classifique os itens abaixo em verdadeiros ou falsos.
I. Toda matriz nula é simétrica.
II. Toda matriz identidade é simétrica.
III. Toda matriz simétrica é uma matriz identidade.
IV. Toda matriz que é igual a sua transporta é uma matriz simétrica.
V. Existe matriz simétrica que não é uma matriz quadrada.
A) Dois itens verdadeiros.
B) Um item verdadeiro.
C) Quatro itens verdadeiros.
D) Três itens verdadeiros.
E) Todos os itens são verdadeiros.
Alternativa A.
I. Toda matriz nula é simétrica. (falso)
Existem matrizes nulas que não são quadradas, logo não são simétricas.
II. Toda matriz identidade é simétrica. (verdadeiro)
Como os elementos fora da diagonal principal são iguais a zero, não há possibilidade de haver \(a_{ij}\neq a_{ji}\).
III. Toda matriz simétrica é uma matriz identidade. (falso)
Existem matrizes simétricas com elementos da diagonal principal diferentes de 1, logo não são simétricas.
IV. Toda matriz que é igual a sua transporta é uma matriz simétrica. (verdadeiro)
Essa é a definição de matriz simétrica.
V. Existe matriz simétrica que não é uma matriz quadrada. (falso)
É uma consequência que a matriz simétrica seja quadrada.
-
Questão 12
Observe as matrizes a seguir e julgue os itens.
\(M=\left(\begin{matrix}4&7&9\\8&4&6\\9&0&9\\\end{matrix}\right)\)
\(B=\left(\begin{matrix}6&8&9\\8&4&5\\9&5&9\\\end{matrix}\right)\)
\(C=\left(\begin{matrix}6&-1&9\\8&4&-1\\9&8&9\\\end{matrix}\right)\)
I. A matriz M é simétrica.
II. A matriz B é simétrica.
III. A matriz C é simétrica.
IV. Nenhuma das matrizes acima é simétrica.
A) Dois itens verdadeiros.
B) Um item verdadeiro.
C) Quatro itens verdadeiros.
D) Três itens verdadeiros.
E) Todos os itens são verdadeiros.
Alternativa B.
I. A matriz M é simétrica. (falso)
M não é uma matriz simétrica, pois os números 7 e 8 são diferentes, além de 6 e 0 serem diferentes. Esses são os elementos que deveriam ser iguais.
II. A matriz B é simétrica. (verdadeiro)
Os elementos fora da diagonal principal são vistos como espelhados por ela.
III. A matriz C é simétrica. (falso)
C não é uma matriz simétrica, pois os números -1 e 8 são diferentes. Esses são os elementos que deveriam ser iguais.
IV. Nenhuma das matrizes acima é simétrica. (falso)
O item II ser verdadeiro torna esse item falso.