Exercícios sobre a relação entre parábola e coeficientes de uma função do segundo grau
Respondendo a estes exercícios, é possível testar seus conhecimentos sobre a relação entre parábola e coeficientes de uma função do segundo grau.
Publicado por: Luiz Paulo Moreira SilvaQuestões
-
Questão 1
A respeito dos coeficientes de uma função do segundo grau do tipo f(x) = ax2 + bx + c e da relação entre eles e o gráfico da função, assinale a alternativa correta.
a) O coeficiente “a” determina apenas a abertura da parábola.
b) O coeficiente “b” determina o ponto de encontro entre a parábola e o eixo y.
c) O coeficiente “c” determina a concavidade da parábola.
d) O coeficiente “a” determina a concavidade da parábola.
e) O coeficiente “b” determina a concavidade da parábola.
Em uma função do tipo f(x) = ax2 + bx + c, o coeficiente “a” determina a concavidade e a abertura da parábola que a representa. Já o coeficiente “c” determina o ponto de encontro entre a parábola e o eixo y.
Alternativa D
-
Questão 2
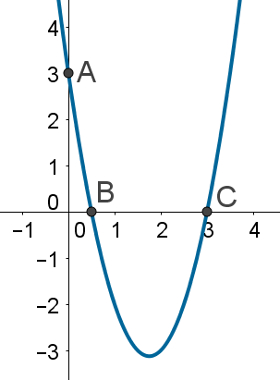
A partir da análise das informações no gráfico a seguir, referente a uma função do segundo grau, assinale a alternativa correta.
a) Os pontos A, B e C são as raízes da função.
b) O ponto B é o ponto de encontro entre a função e o eixo y.
c) O ponto C é o ponto de encontro entre a função e o eixo y.
d) As raízes dessa função são: x = 1 e x = 3.
e) O coeficiente “a” dessa função é positivo.
a) Incorreta!
Apenas os pontos B e C são raízes dessa função, pois as raízes são os pontos de encontro entre o gráfico da função e o eixo x.
b) Incorreta!
O ponto B é raiz, portanto não pode ser ponto de encontro com o eixo y.
c) Incorreta!
O ponto C é raiz, portanto não pode ser ponto de encontro com o eixo y.
d) Incorreta!
A função não toca o ponto (1, 0). Portanto, o ponto B, que é raiz, não está sobre x = 1.
e) Correta!
Alternativa E
-
Questão 3
Dada a função f(x) = x2 + 9, analise as alternativas a seguir e assinale aquela que for correta.
a) As raízes da função são x = 3 e x = – 3.
b) Como o discriminante é negativo, não é possível encontrar as raízes dessa função considerando apenas o conjunto dos números reais.
c) Como o discriminante é negativo e o coeficiente a é positivo, então essa função possui ponto de máximo.
d) O discriminante dessa função é igual a zero, portanto, ela possui apenas uma raiz real.
e) O gráfico dessa função toca o eixo x apenas uma vez.
Primeiramente, vale calcular o discriminante da função, já que a questão é teórica.
Δ = b2 – 4·a·c
Δ = 02 – 4·1·9
Δ = 0 – 36
Δ = – 36
a) Incorreta!
O discriminante é negativo, portanto, não é possível encontrar raízes reais para essa função.
b) Correta!
c) Incorreta!
Nessas circunstâncias, a função possui ponto de mínimo.
d) Incorreta!
O discriminante da função não é igual a zero.
e) Incorreta!
Como o discriminante da função é diferente de zero, então ela não encontra o eixo x em nenhum ponto, pois não possui raízes reais.
Alternativa B
-
Questão 4
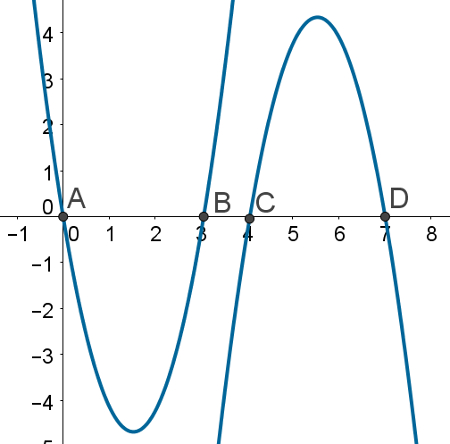
Observe os dois gráficos a seguir para assinalar a alternativa correta:
a) Ambas as funções representadas pelos gráficos possuem discriminante negativo.
b) Ambas as funções representadas pelos gráficos possuem discriminante positivo. Entretanto, o coeficiente “a” é positivo apenas em uma delas.
c) Somente uma das funções possui coeficiente “b”, uma vez que apenas uma delas toca o eixo y.
d) Ambas as funções possuem raízes reais, o que significa que o discriminante de ambas é igual a zero.
e) Ambas as funções possuem ponto de máximo.
a) Incorreta!
O discriminante negativo garante que funções do segundo grau não possuem raízes reais, que, por sua vez, são os pontos de encontro entre a função e o eixo x. Entretanto, ambas as funções apresentam duas raízes. Portanto, os discriminantes delas são positivos.
b) Correta!
c) Incorreta!
O coeficiente “b” não determina o ponto de encontro com o eixo y. Além disso, nada garante que uma das funções não toque o eixo y.
d) Incorreta!
Se o discriminante é zero, a função possui apenas uma raiz real. Ambas as funções apresentadas possuem duas raízes reais.
e) Incorreta!
Uma das funções possui ponto de máximo e a outra de mínimo.
Alternativa B