1. Home
  2. Exercícios de Matemática
  3. Exercícios sobre sistema de numeração decimal

Exercícios sobre sistema de numeração decimal

Esta lista de exercícios vai testar o seu conhecimento sobre o sistema de numeração decimal, com questões resolvidas sobre as ordens e classes que utilizamos cotidianamente.

Publicado por: Raul Rodrigues de Oliveira

Questões

Imprimir icone Imprimir
  1. Questão 1

    (Enem - 2014) Os incas desenvolveram uma maneira de registrar quantidades e representar números utilizando um sistema de numeração decimal posicional: um conjunto de cordas com nós denominado quipus. O quipus era feito de uma corda matriz, ou principal (mais grossa que as demais), na qual eram penduradas outras cordas, mais finas, de diferentes tamanhos e cores (cordas pendentes). De acordo com a sua posição, os nós significavam unidades, dezenas, centenas e milhares. Na Figura 1, o quipus representa o número decimal 2 453. Para representar o “zero” em qualquer posição, não se coloca nenhum nó.

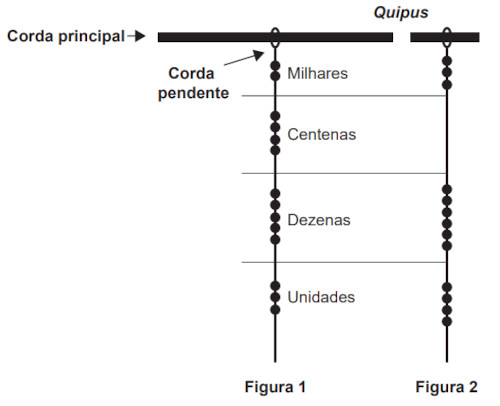
    O número da representação do quipus da Figura 2, em base decimal, é:

    A) 364.

    B) 463.

    C) 3 064.

    D) 3 640.

    E) 4 603.

  2. Questão 2

    (Enem 2016) O ábaco é um antigo instrumento de cálculo que usa notação posicional de base dez para representar números naturais. Ele pode ser apresentado em vários modelos, um deles é formado por hastes apoiadas em uma base. Cada haste corresponde a uma posição no sistema decimal e nelas são colocadas argolas; a quantidade de argolas na haste representa o algarismo daquela posição. Em geral, colocam-se adesivos abaixo das hastes com os símbolos U, D, C, M, DM e CM, que correspondem, respectivamente, a unidades, dezenas, centenas, unidades de milhar, dezenas de milhar e centenas de milhar, sempre começando com a unidade na haste da direita e as demais ordens do número no sistema decimal nas hastes subsequentes (da direita para esquerda), até a haste que se encontra mais à esquerda.

    Entretanto, no ábaco da figura, os adesivos não seguiram a disposição usual.

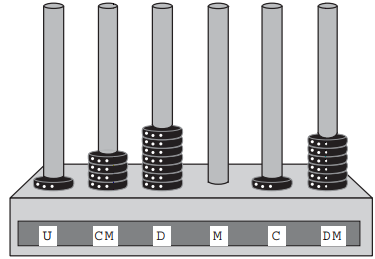
    Nessa disposição, o número que está representado na figura é:

    A) 46 171.

    B)147 016

    C) 171 064.

    D) 460 171.

    E) 610 741.

  3. Questão 3

    Realizando a decomposição de um número, encontramos a soma 50000 + 300 + 20 + 1. O número decomposto foi:

    A) 53210.

    B) 53021.

    C) 50321.

    D) 500321.

  4. Questão 4

    No número 153902, o valor posicional do algarismo 9 é:

    A) 9.

    B) 9.

    C) 900.

    D) 9000.

    E) 90000.

  5. Questão 5

    Nos números 1320, 203 e 2932, o valor posicional do algorismo 3 é, respectivamente:

    A) centena, dezena e unidade.

    B) unidade, dezena e centena.

    C) dezena, unidade e centena.

    D) centena, unidade e dezena.

    E) dezena, centena e unidade.

  6. Questão 6

     Em um trabalho da escola, Márcio e Tiago estavam no mesmo grupo, então Márcio anotou o telefone de Tiago em um papel de anotações. Porém, por descuido de Márcio, durante o lanche, ele derramou katchup em um dos dígitos conforme a imagem a seguir:

    O número que está manchado corresponde à:

    A) unidade.

    B) dezena.

    C) centena.

    D) unidade de milhar.

    E) dezena de milhar. 

  7. Questão 7

    Na campanha de vacinação de uma cidade, foram vacinadas 380.210 crianças. O nome desse número por extenso é:

    A) trezentos e oitenta mil e duzentos e dez.

    B) trinta e oito mil e duzentos e dez.

    C) trezentos e oitenta e dois mil e cem.

    D) trezentos milhões duzentos e dez mil

    E) trezentos e oitenta duzentos e dez mil.

  8. Questão 8

     Sobre o número 123.456.789.201, podemos afirmar que:

    A) 789 pertence à classe das unidades simples.

    B) 123 pertence à classe das dezenas.

    C) 456 pertence à classe dos milhões.

    D) 201 pertence à classe dos milhares. 

  9. Questão 9

    Um padeiro produziu 1423 pães durante a semana. Esse número é formado por:

    A) 1 unidade de milhar, 4 centenas, 2 dezenas e 3 unidades.

    B) 1 unidade de milhão, 4 unidades de milhar, 2 dezenas e 3 unidades.

    C) 1 centena, 4 dezenas e 2 unidades.

    D) 1 unidade de milhar, 4 centenas, 3 dezenas e 2 unidades.

  10. Questão 10

    (Ipad) Dentre os números 2.501, 4.235, 1.536, 4.057, 30.597 e 41.500, quantos têm o algarismo 5 ocupando a ordem das centenas?

    A) 1

    B) 2

    C) 3

    D) 4

    E) 5

  11. Questão 11

    (FCC – SP) Um número tem dois algarismos, sendo y o algarismo das unidades e x o algarismo das dezenas. Se colocarmos o algarismo 2 à direita desse número, o novo número será:

    Número: xy

    Novo número: xy2

    A) x + y + 2

    B) 200 + 10·y + x

    C) 100·x + 10·y + 2

    D) 100·y + 10·x + 2

  12. Questão 12

    A quantidade de números com três algarismos diferentes que podemos formar com os números 1,4 e 5 usando os três algarismos são:

    A) 2.

    B) 3.

    C) 4.

    D) 5.

    E) 6.