Exercícios sobre Soma dos Termos de uma PG Infinita
Estes exercícios sobre soma dos termos de uma PG infinita podem ser resolvidos por meio de uma única fórmula que adiciona os elementos conhecidos da sequência.
Publicado por: Amanda Gonçalves RibeiroQuestões
-
Questão 1
Determine a soma dos termos da PG infinita
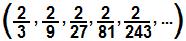 .
.Vamos determinar a razão q dessa PG. Para tanto, basta dividir um termo pelo seu antecessor. Considerando o 1° e 2° termos da sequência, temos:
q = a2
a1
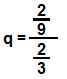
q = 2 . 3
9 2
q = 3
9
q = 1
3Agora que conhecemos a razão, vamos aplicá-la à fórmula da soma dos termos de uma PG infinita, sabendo que a1 = 2/3:
S = a1
1 – q
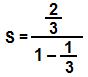
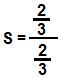
S = 1Portanto, a soma dos termos da PG infinita é 1.
-
Questão 2
Resolva a equação a seguir:
x + 2x + 4x + ... = 15
5 25Observe que o primeiro membro da equação é uma PG infinita. Logo, para resolvê-la, precisamos determinar a soma dos termos dessa sequência. Primeiramente, determinamos a razão:
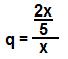
q = 2x . 1
5 x
q = 2
5Vamos agora determinar a soma dos termos:
S = a1
1 – q
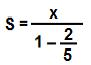
.jpg)
S = x . 5
3
S = 5x
3Substituiremos todo o primeiro membro da equação pelo valor da soma encontrada:
x + 2x + 4x + ... = 15
5 25
5x = 15
3
5x = 15 · 3
5x = 45
x = 45
5
x = 9Portanto, o resultado da equação é x = 9.
-
Questão 3
(UFLA) A soma dos elementos da sequência numérica infinita (3; 0,9; 0,09; 0,009; …) é:
a) 3,1
b) 3,9
c) 3,99
d) 3,999
e) 4
Observe que na sequência (3; 0,9; 0,09; 0,009; …) o primeiro termo não obedece ao padrão estabelecido entre os demais termos. Por isso, vamos separá-lo da sequência e no fim da resolução adicioná-lo à soma encontrada.
Considerando a nova sequência (0,9; 0,09; 0,009; …), vamos calcular o quociente dos termos a2 = 0,09 e a1 = 0,9 para determinar a razão dessa PG:
q = a2
a1
q = 0,09
0,9
q = 0,1Como q = 0,1 e a1 = 0,9, podemos calcular a soma dos termos dessa sequência:
S = a1
1 – q
S = 0,9
1 – 0,1
S = 0,9
0,9
S = 1A soma dos termos de (0,9; 0,09; 0,009; …) é 1. Somando o termo dispensado no início, obtemos S = 4, o que nos indica que a alternativa correta é a letra e.
-
Questão 4
(Cefet - MG) Se 1 + x2 + x4 + … + x2n + … = 25 , então x é igual a:
16a) 3
5b) – 3
5c) ± 3
5d) ± 5
4e) 5
4Podemos considerar que o primeiro membro da equação é uma PG infinita cujos termos estão sendo somados. Vamos determinar a razão:
q = x²
1
q = x²Vamos agora determinar a soma dos termos:
S = a1
1 – q
S = 1
1 – x²Substituindo o primeiro membro da equação pelo valor da soma S encontrado, teremos:
1 + x2 + x4 + … + x2n + … = 25
16
1 = 25
1 – x² 16
(1 – x²) · 25 = 16
25 – 25x² = 16
– 25x² = 16 – 25
– 25x² = – 9
25x² = 9
x² = 9
25
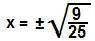
x = ± 3
5Portanto, a alternativa correta é a letra c.